
����Ŀ���ۺ���ʵ��
�����龳��
���ۺ���ʵ�����ϣ���ʦ��ͬѧ���ԡ����������εļ�ƴ��Ϊ���չ��ѧ�����ͼ1���ڡ�ABC�У�AB��AC��10cm��BC��16cm������ABC��BC���ϵ�����AD�������õ���ABD�͡�ACD��
�������֣�
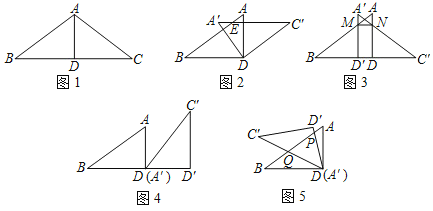
��1����ѧС�齫ͼ1�еġ�ACD�Ե�DΪ��ת���ģ�����ʱ�뷽����ת��ʹ��A'C'��AD���õ�ͼ2��A'C'��AB���ڵ�E�����ı���BEC'D����״���� ����
��2������С�齫ͼ1�еġ�ACD��DB����ƽ�ƣ�A'D'��AB���ڵ�M��A'C'��AD���ڵ�N���õ�ͼ3���ж��ı���MNDD'����״����˵�����ɣ�
ʵ��̽����
��3������С���ַ��֣�����2�����߶�DD'�ij�Ϊacmʱ��ͼ3�е��ı���MNDD'���Ϊ�����Σ���a��ֵ��
��4������С���ְ�ͼ1�еġ�ACD�ŵ���ͼ4��ʾ��λ�ã���A�Ķ�Ӧ��A'���D�غϣ���D�Ķ�Ӧ��D'��BD���ӳ����ϣ��ٽ���A'C'D'�Ƶ�D��ʱ����ת����ͼ5��ʾ��λ�ã�DD'��AB�ڵ�P��DC'��AB�ڵ�Q��DP��DQ����ʱ�߶�AP�ij����� ��cm��
���𰸡�(1)���Σ�(2)�ı���MNDD'�Ǿ��Σ����ɼ�������(3)![]() ��(4)
��(4)![]()
��������
�������֣�
��1���ɵ��������ε����ʿɵá�B=��C��BD=CD=8cm����BAD=��CAD������ǵ����ʿɵá�ADC'=��BAD���ɵ�AB��C'D����֤�ı���BDC'E��ƽ���ı��Σ���BD=C'D����֤�ı���BEC'D�����Σ�
��2���ɡ�ASA����֤��MDB'�ա�NDC'���ɵ�DN=MD'����ƽ�����ʿɵ�MD'��DN����֤�ı���MNDD'��ƽ���ı��Σ��ҡ�BD'M=90�㣬��֤�ı���MNDD'�Ǿ��Σ�
ʵ��̽����
��3���������ε����ʿɵ�D'M��DN��D'M=D'D=acm�������������ε����ʿ���⣻
��4������D��DG��AB�ڵ�G��ͨ��֤����DQP�ס�AQD������AQ=AD=6��ͨ��֤����DGA�ס�BDA���ɵ�![]() ������AG�ij���������⣮
������AG�ij���������⣮
�⣺�������֣�
��1����ͼ1����AB��AC��10cm��BC��16cm��
���B����C��BD��CD��8cm����BAD����CAD��
�ߡ�ACD�Ե�DΪ��ת���ģ�����ʱ�뷽����ת��
��C'D��BD��
��AD��BD��A'C'��AD��
��A'C'��BD����ADC'��90�㩁��C'��
���ADC'��90�㩁��B���ҡ�BAD��90�㩁��B��
���ADC'����BAD��
��AB��C'D��
���ı���BDC'E��ƽ���ı��Σ�
��BD��C'D��
���ı���BEC'D�����Σ�
�ʴ�Ϊ�����Σ�
��2����ͼ3���ı���MNDD'�Ǿ��Σ�
�������£�
��BD��CD��
��BD'��CD���ҡ�B����C'����MD'B����NDC'
���MDB'�ա�NDC'��ASA��
��MD'��ND��
�ߡ�ACD��DB����ƽ�ƣ�
��MD'��DN��
���ı���MNDD'��ƽ���ı��Σ�
�ߡ�BD'M��90�㣬
���ı���MNDD'�Ǿ��Σ�
��3����ͼ�Σ�1���ɵ�AB��10cm��BD��8cm��
��AD��![]() ��
��![]() ��6cm��
��6cm��
���ı���MNDD'Ϊ�����Σ�
��D'M��DN��D'M��D'D��acm��
���BD'M�ס�BDA��
��![]() ��
��
��![]() ��
��
��a��![]() ��
��
��4����ͼ5������D��DG��AB�ڵ�G��
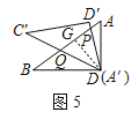
��DP��DQ��
���DQP����DPQ��QG��PG��
�֡ߡ�A����PDQ��
���DQP�ס�AQD��
���ADQ����DPQ��
���ADQ����AQD��
��AQ��AD��6��
�ߡ�A����A����DGA����BDA��
���DGA�ס�BDA��
��![]() ��
��
��![]() ��
��
��AG��![]() ��
��
��GQ��AQ��AG��6��![]() ��
��![]() ��
��
��PG��QG��![]() ��
��
��AP��AG��PG��![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
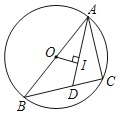
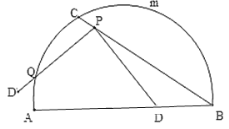
����Ŀ����ͼ����O����ABC�����Բ��AB�ǡ�O��ֱ����IΪ��ABC�����ģ�AI���ӳ��߽�BC��D����OI��AD����sin��CAD��ֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB��AC
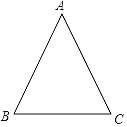
��1������һ��P��ʹ��PΪ��ABC�����ԲԲ�ģ���������ͼ�ۼ�����д������
��2������A��50�������PBC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C��![]() ��һ���㣬D����AB�ϵ�һ���㣬P����CB�ϵ�һ����.����DP�����߶�PD�Ƶ�P˳ʱ����ת
��һ���㣬D����AB�ϵ�һ���㣬P����CB�ϵ�һ����.����DP�����߶�PD�Ƶ�P˳ʱ����ת![]() �õ��߶�
�õ��߶�![]() .����
.����![]() ��
��![]() ���ڵ�Q.��֪
���ڵ�Q.��֪![]() ����P��C�����ľ���Ϊxcm��P��D�����ľ���
����P��C�����ľ���Ϊxcm��P��D�����ľ���![]() ��P��Q����ľ���Ϊ
��P��Q����ľ���Ϊ![]() .
.
Сʯ����ѧϰ�����ľ��飬�ֱ�Ժ���![]() ��
��![]() �����Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������Сʯ��̽�����̣��벹��������
�����Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������Сʯ��̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���![]() ��
��![]() ����x�ļ����Ӧֵ��
����x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����������Ӧ�ĵ�![]() ��
��![]() ������������
������������![]() ��
��![]() ��ͼ��
��ͼ��
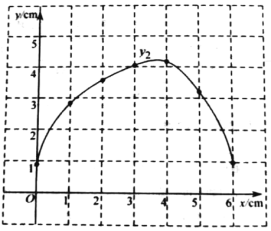
��3����Ϻ���ͼ������⣺����DQ������DPQΪ����������ʱ��PC�ij���ԼΪ_____cm.���������һλС����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1��kx+b�뷴��������y2��![]() ��ͼ����A��2��3����B��6��n�����㣬��x�ᡢy��ֱ���C��D���㣮
��ͼ����A��2��3����B��6��n�����㣬��x�ᡢy��ֱ���C��D���㣮
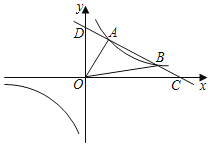
��1����һ�κ����뷴���������Ľ���ʽ��
��2����xΪ��ֵʱ��y1��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ���AC����һ��E����CE��4AE����F��DC���ӳ����ϣ�����EF������E��EG��EF����CB���ӳ����ڵ�G������GF���ӳ�����AC���ӳ����ڵ�P����AB��5��CF��2�����߶�EP�ij���_____��
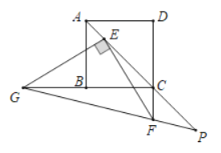
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
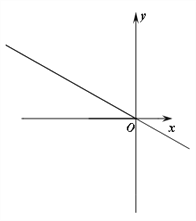
����Ŀ����֪���κ���![]() ��0���ĶԳ�����x�ύ�ڵ�B����ֱ��l��
��0���ĶԳ�����x�ύ�ڵ�B����ֱ��l��![]() ���ڵ�C����A�Ǹö��κ���ͼ����ֱ��l�ڵڶ����Ľ��㣬��D�������ߵĶ��㣬��֪AC��CO��1��2����DOB��45�㣬��ACD�����Ϊ2��
���ڵ�C����A�Ǹö��κ���ͼ����ֱ��l�ڵڶ����Ľ��㣬��D�������ߵĶ��㣬��֪AC��CO��1��2����DOB��45�㣬��ACD�����Ϊ2��
(1) �������ߵĺ�����ϵʽ��
(2) ����PΪ�����߶Գ����ϵ�һ���㣬����POC��45�������P����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��õ�����������ˮ�ʣ����������������۹�˾�������� 10 ̨��ˮ�����豸������ A��B �����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±���
A �� | B �� | |
�۸���Ԫ/̨�� | a | b |
������ˮ�����֣��£� | 240 | 200 |
�����飺����һ̨ A ���豸�ȹ���һ̨ B ���豸�� 2 ��Ԫ������ 2 ̨ A ���豸�ȹ��� 3 ̨ B ���豸�� 6 ��Ԫ��
��1���� a��b ��ֵ��
��2����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ��� 105 ��Ԫ������Ϊ�ù�˾ ���ļ��ֹ�����
��3���ڣ�2���ʵ������£���ÿ��Ҫ��������������ˮ�������� 2040 �֣�Ϊ�˽� Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����AC���ң�CD����O�����ߣ�CΪ�е㣬AD��CD�ڵ�D��
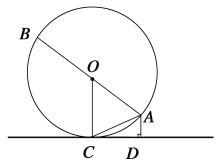
��֤����1����AOC=2��ACD����2��AC2��AB��AD��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com