
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,
的中点,![]() 过
过![]() 的中点
的中点![]() 并与
并与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() 的面积为
的面积为![]() ,则四边形
,则四边形![]() 的面积=______.
的面积=______.
【答案】![]()
【解析】
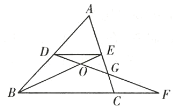
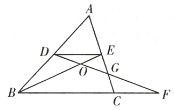
由点D、E分别是边AB、AC的中点,可得DE∥BC,DE=![]() BC,即可得△ADE∽△ABC与△ODE∽△OFB,又由EC的中点是G,则可得△DEG≌△FCG,然后由相似三角形的面积比等于相似比的平方与等高三角形的面积比等于对应底的比即可求得答案.
BC,即可得△ADE∽△ABC与△ODE∽△OFB,又由EC的中点是G,则可得△DEG≌△FCG,然后由相似三角形的面积比等于相似比的平方与等高三角形的面积比等于对应底的比即可求得答案.
解:∵点D、E分别是边AB、AC的中点,
![]()
![]()
![]()
∵△ADE的面积为S,
∴S△ABC=4S,
∵DE∥BC,
∴△ODE∽△OFB,∠EDG=∠F,∠DEG=∠GCF,
![]()
又EG=CG,
∴△DEG≌△FCG(AAS),
∴DE=CF,
∴BF=3DE,
∵DE∥BC,
∴△ODE∽△OFB
![]()
∵AD=BD,
∴S△BDE=S△ADE=S,
∵AE=CE=2EG,
![]()
![]()
![]()
![]()
∵S四边形DBCE=S△ABC-S△ADE=3S,
∴S四边形OBCG=S四边形DBCE-S△BDE-S△OEG=3S-S-![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据![]() ,3,
,3,![]() ,2,
,2,![]() 中可以作为线段AQ长的有_____个.
中可以作为线段AQ长的有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
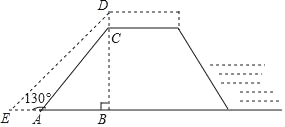
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
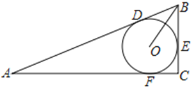
【题目】如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F,若AD=10,BC=5,则OB的长为( )
A.4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程ax2+(a+2)x+9a=0有两个不等的实数根x1,x2,且x1<1<x2,那么a的取值范围是( )
A.﹣![]() <a<
<a<![]() B.a>
B.a>![]() C.a<﹣
C.a<﹣![]() D.﹣
D.﹣![]() <a<0
<a<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)直接写出BC的长是 ,点D的坐标是 ;
(2)证明:△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com