
分析 (1)把要求的式子先去掉括号,再合并同类项即可得出答案;
(2)先把分式方程化成整式方程,求出x的值,再进行检验即可得出答案.
解答 解:(1)原式=9x2-6xy+y2-4x2-4xy-y2+5xy-5x2
=(9x2-4x2-5x2)+(-6xy-4xy+5xy)+(y2-y2)
=-5xy;
(2)$\frac{x}{x-2}-1=\frac{8}{{x}^{2}-4}$,
去分母得:x(x+2)-x2+4=8,
去括号得:x2+2x-x2+4=8,
移项合并得:2x=4,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了整式的混合运算和解分式方程,关键是根据整式的混合运算把要求的式子进行化简,把分式方程化成整式方程再求解,注意分式方程一定要检验.


科目:初中数学 来源: 题型:解答题
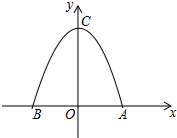 某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2.
某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种客车 | 乙种客车 | |
| 载客量(座/辆) | 60 | 45 |
| 租金(元/辆) | 550 | 450 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
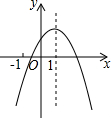 如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com