练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在?ABCD中，BC=2CD，点M、N分别在BC、CD边上，AM与BN交于点E．若∠C=∠AEN，BN=5
    		5
    ，则AM的长为
     
    ．
    考点：相似三角形的判定与性质,平行四边形的性质
    专题：
    分析：易证△ABM∽△AEB和△BEM∽△BCN根据相似三角形对应边比例等于相似比即可求得AM的值．
    解答：解：∵∠C=∠AEM，
    ∴∠AEB=∠ABM（∠ABM+∠C=180°），
    ∴△ABM∽△AEB，
    ∴AM：AB=BM：BE，∠ABN=∠AMB，①
    ∵∠CNB=∠ABN=∠AMB，
    ∴△BEM∽△BCN
    ∴NB：BM=BC：BE，②
    由①②得：AM：AB=BN：BC，
    ∴AM=
    AB•BN
    BC

    ∵2AB=BC，
    ∴AM=
    BN
    2
    =
    5
    		5
    2
    ．
    点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例等于相似比的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    若a-2b=0，且ab=18，则a2+2ab+4b2=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：（3x-5y2）（-3x-5y2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    幻方：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC的高AD、BE交于点H，若BH=AC，证明：
    （1）∠ABC=45°；
    （2）DH=DC；
    （3）∠CED=45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们知道：
    1+3=4=22；
    1+3+5=9=32；
    1+3+5+7=16=42；
    1+3+5+7+9=25=52．根据前面各式规律，可以猜测：
    1+3+5+7+9+…+（2n-1）=
     
    ．（其中n为自然数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

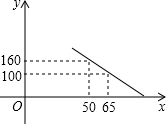    大学生王强积极响应“自主创业”的号召，准备投资销售一种进价为每件40元的小家电．通过试销发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示．求y与x的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，D为BC上的一点，且S△ACD=S△ABD，则AD为（　　）
    A、高B、中线
    C、角平分线D、不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB=a，则图中阴影部分的面积为
     
    ．

    查看答案和解析>>

    同步练习册答案