
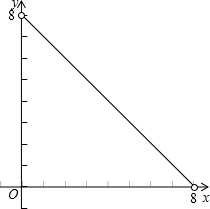
 矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm
矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm| x | 0 | 8 |
| y=8-x | 8 | 0 |
| 6(8-x) |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 序号 | 方程 | 方程的解 |
| 1 | x2-2x-3=0 | x1=-1,x2=3 |
| 2 | x2-4x-12=0 | x1=-2,x2=6 |
| 3 | x2-6x-27=0 | x1= |
查看答案和解析>>
科目:初中数学 来源: 题型:
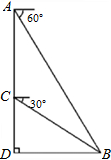 小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com