
已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
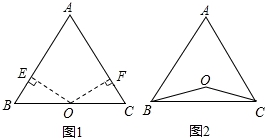
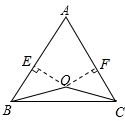
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
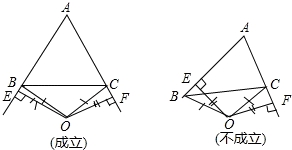
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
【考点】全等三角形的判定与性质.
【专题】几何综合题.
【分析】(1)求证AB=AC,就是求证∠B=∠C,可通过构建全等三角形来求.过点O分别作OE⊥AB于E,OF⊥AC于F,那么可以用斜边直角边定理(HL)证明Rt△OEB≌Rt△OFC来实现;
(2)思路和辅助线同(1)证得Rt△OEB≌Rt△OFC后,可得出∠OBE=∠OCF,等腰△ABC中,∠ABC=∠ACB,因此∠OBC=∠OCB,那么OB=OC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC.
【解答】(1)证明:过点O分别作OE⊥AB于E,OF⊥AC 于F,
于F,
由题意知,
在Rt△OEB和Rt△OFC中
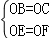
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
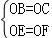
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如示例图)
【点评】本题的关键是通过辅助线来构建全等三角形.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
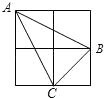
如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知m+a=n+b,利用等式的性质可变形为m=n,那么a、b必符合条件( )
A. a=-b; B. a=b; C. –a=b; D. a、b为任意有理数或整式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com