
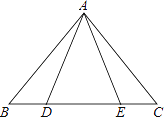
����Ŀ�������龳����ͼ1����D�ǡ�ABC���һ�㣬��E��BC�ߵ��ӳ����ϣ�BDƽ�֡�ABC��CDƽ�֡�ACE����̽����D���A��������ϵ��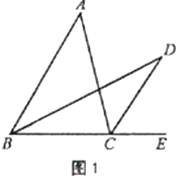
��1������̽����
��ͼ2������ABC�ǵȱ������Σ������������䣬���D����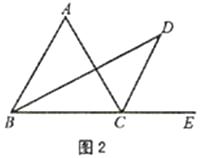
��ͼ3������ABC�ǵ��������Σ����ǡ�A��100�㣬�����������䣬���D����������ͼ�У���D���A�����ı�����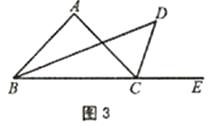
��2������֤����
��ͼ1����ABCΪһ�������Σ��ڣ�1���л�õġ�D���A�Ĺ�ϵ�Ƿ�����������������ͼ1֤����Ľ��ۣ�����������˵�����ɣ�
���𰸡�
��1��30�㣻50�㣻1��2
��2���⣺����.
��BDƽ�֡�ABC��
���ABD=��DBC��
��CDƽ�֡�ACE��
���ACD=��DCE��
�ߡ�ACE�ǡ�ABC����ǣ�
���ACE=��ABC����A�� ��2��DCE =2��DBC+��A��
�ߡ�DCE�ǡ�BCD����ǣ�
���DCE����DBC����D��
��2��DBC+��A��2����DBC����D����
���D�� ![]() ��A������D����A��1:2
��A������D����A��1:2
���������⣺(1)��30��50��1��2�� (1���ٸ��ݽ�ƽ���ߵĶ���ó���ABD=��DBC=30�㣬��ACD=��DCE=60�㣬���������ε���Ƕ����ó���DCE=��DBC+��D ,�Ӷ��ó���D=30�� ;�ڸ��ݵ��������ε����ʵó���ABC=40�� ,���ݽ�ƽ���ߵĶ���ó���ABD=��DBC=20��,���������ε���Ƕ����ó���ACE=��A����ABC��140�� ,��ACD=��DCE=70�� ,���������ε���Ƕ����ó���DCE=��DBC+��D ,�Ӷ��ó���D=50�� ;
(2�����ݽ�ƽ���ߵĶ���ó���ABD=��DBC����ACD=��DCE�����������ε���Ƕ����ó���ACE=��ABC����A�� ��2��DCE =2��DBC+��A����DCE����DBC����D���Ӷ��ó�2��DBC+��A��2����DBC����D��������D����A��1:2 ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������y=kx��k�dz�����k��0����ͼ���ڶ��������ޣ���k��ֵ��������д��һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ��ֱ������ϵ�У�ֱ�� ![]() ��x�ύ�ڵ�A����y�ύ��B����ֱ��y��x���ڵ�C��
��x�ύ�ڵ�A����y�ύ��B����ֱ��y��x���ڵ�C��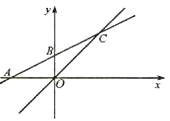
��1����A��B��C��������ꣻ
��2�����AOC�������
��3����֪��P��x���������ϵ�һ�㣬����COP�ǵ��������Σ�ֱ��д��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�У�AB=AC��D��E����BC�ϣ�Ҫʹ��ABD�ա�ACE����Ҫ����һ��������ijѧϰС���������������ʱ���������¼��ַ����� ��AD=AE����BD=CE����BE=CD���ܡ�BAD=��CAE�����п��е��У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪am=2��an=3����am+2n��ֵ.
����֪(x+y)2=18��(x��y)2=6����xy��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֽƬABCD����ͼ��ʾ�ķ�ʽ�۵���ǡ�õõ�����AECF����AB=3��������AECF�����Ϊ�� ��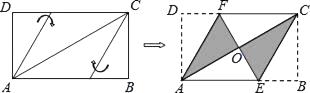
A.1
B.![]()
C.![]()
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Թ���ʵ��һϵ������ũ���Ż����ߺ�ũ�������������ӣ�ij������Ͻ��ׯȥ������˾����루��λ��Ԫ����������
���˾����� | 10500 | 10700 | 10800 | 10900 | 11500 |
��ׯ���� | 1 | 1 | 3 | 3 | 1 |
����ȥ�����ׯ���˾��������λ���ǣ�������
A. 10700 B. 10800 C. 10850 D. 10900
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com