
 如图,点A表示一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=30°,如果在B、C两村庄之间修一条长500m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?
如图,点A表示一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=30°,如果在B、C两村庄之间修一条长500m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?科目:初中数学 来源: 题型:
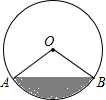 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:
 在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.
在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com