考点:平行线的判定
专题:推理填空题
分析:(1)∠1和∠8是AB、DF被DE所截得到的一对内错角,∠1和∠B是DE、BC被AB所截得到的一对同位角,可得出答案;
(2)∠2和∠4是DE、BC被EF所截得到的一对内错角,∠2和∠CDE是EF、CD被DE所截得到的一对同旁内角,可得出答案;
(3)∠5和∠3是AB、DF被EF所截得到的一对内错角,∠5和∠ADF是AC、EF被DF所截得到的一对同旁内角,可得出答案;
(4)∠8和∠6是DE、BC被DF所截得到的一对内错角,∠C和∠EFC是EF、CD被BC所截得到的一对同旁内角,可得出答案.
解答:解:
(1)∵∠1和∠8是AB、DF被DE所截得到的一对内错角,
∴当∠1=∠8时AB∥DF,
∵∠1和∠B是DE、BC被AB所截得到的一对同位角,
∴当∠1=∠B=180°时DE∥BC,
故答案为:∠8;∠B;
(2)∵∠2和∠4是DE、BC被EF所截得到的一对内错角,
∴当∠2=∠4时DE∥BC,
∵∠2和∠CDE是EF、CD被DE所截得到的一对同旁内角,
∴当∠2+∠CDE=180°时EF∥CD,
故答案为:∠4;∠CDE;
(3)∵∠5和∠3是AB、DF被EF所截得到的一对内错角,
∴当∠5=∠3时AB∥DF,
∵∠5和∠ADF是AC、EF被DF所截得到的一对同旁内角,
∴当∠5+∠ADF=180°时DC∥EF,
故答案为:∠3;∠ADF;
(4)∵∠8和∠6是DE、BC被DF所截得到的一对内错角,
∴当∠8=∠6时DE∥BC,
∵∠C和∠EFC是EF、CD被BC所截得到的一对同旁内角,
∴当∠C+∠EFC=180°时EF∥CD,
故答案为:∠6;∠EFC.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

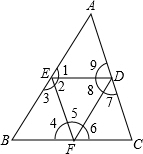 如图,填空:
如图,填空:

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案