
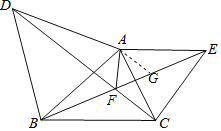
【题目】如图,△ABD,△ACE都是等边三角形,BE,DC相交于点F,连接AF.
(1)求证:BE=DC;
(2)求证:AF平分∠DFE.

【答案】(1)见解析;(2)见解析
【解析】
(1)根据等边三角形的性质和全等三角形的判定和性质解答.
(2)根据全等三角形的判定和性质以及角平分线的判定解答即可.
解:(1)∵△ABD和△ACE都是等边三角形,
∴∠DAB=60°,∠CAE=60°,
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,
∵在△ADC与△ABE中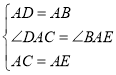 ,
,
∴△ADC≌△ABE(SAS),
∴BE=CD;
(2)在BE上截取EG=CF,连接AG,
由(1)的证明,知△ADC≌△ABE,
∴∠AEB=∠ACD,即∠AEG=∠ACF,
∵AE=AC,
在△AEG与△ACF中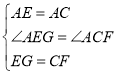 ,
,
∴△AEG≌△ACF(SAS),
∴∠AGE=∠AFC,AG=AF,
∵∠AGE=∠AFC
∴∠AGF=∠AFD,
∵AG=AF
∴∠AGF=∠AFG,
∴∠AFD=∠AFG,
∴AF平分∠DFE.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
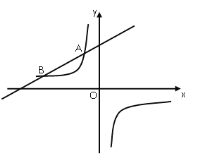
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高学生的消防意识,举行了消防知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
(1)这次知识竞赛共有多少名学生?
(2)“二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() 的度数是 ;
的度数是 ;
(2)若![]() ,
,![]() 的周长是
的周长是![]() .
.
①求![]() 的长度;
的长度;
②若点![]() 为直线
为直线![]() 上一点,请你直接写出
上一点,请你直接写出![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B坐标为(-3,0),点A是y轴正半轴上一点,且AB=5,点P是x轴上位于点B右侧的一个动点,设点P的坐标为(m,0)

(1)点A的坐标为( )
(2)当△ABP是等腰三角形时,求P点的坐标;
(3)如图2,过点P作PE⊥AB交线段AB于点E,连接OE.若点A关于直线OE的对称点为A',当点A'恰好落在直线PE上时,BE=________(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com