
分析 分两种情形考虑:①如图1中,当高AE在△ABC内时,如图2中,当高AE在△ABC外时,分别画出图形,根据勾股定理即可解决问题.
解答 解:①如图1中,当高AE在△ABC内时,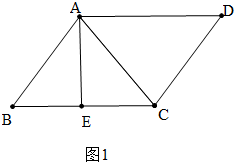
∵$\frac{1}{2}$•BC•AE=$\frac{1}{2}$S平行四边形ABCD=6$\sqrt{3}$,
∴$\frac{1}{2}$×6×AE=6$\sqrt{3}$,
∴AE=2$\sqrt{3}$,
在RT△ABE中,∵AB=4,AE=2$\sqrt{3}$,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴EC=CB-BE=6-2=4.
②如图2中,当高AE在△ABC外时,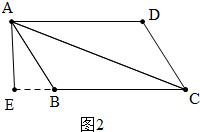
由①可知EB=2,∴CE=EB+BC=2+6=8,
故答案为2或8.
点评 本题考查平行四边形的性质、勾股定理等知识,解题的关键是正确画出图形,有两种情形,考虑问题要全面,属于中考常考题型.


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
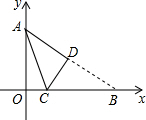 已知OA=6,OB=8,将△AOB沿着某直线CD折叠后如图所示,CD与x轴交于点C,与AB交于点D,则点C坐标是($\frac{7}{4}$,0).
已知OA=6,OB=8,将△AOB沿着某直线CD折叠后如图所示,CD与x轴交于点C,与AB交于点D,则点C坐标是($\frac{7}{4}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
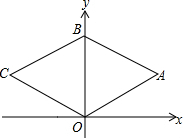 如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.
如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$,1 | B. | -$\frac{1}{2}$,1 | C. | -$\frac{1}{2}$,-1 | D. | $\frac{1}{2}$,-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com