
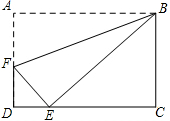
 如图,在矩形ABCD中,AB:BC=2:
如图,在矩形ABCD中,AB:BC=2:| 3 |
 解:(1)∵AB:BC=2:
解:(1)∵AB:BC=2:| 3 |
| 3 |
| 3 |
| 3 |
| 2k | ||
|
2
| ||
| 3 |
| 3 |
| 2k | ||
|
| ||
| 3 |


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
 如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.
如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.查看答案和解析>>
科目:初中数学 来源: 题型:
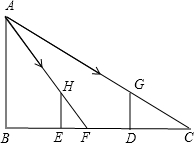 如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.
如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com