

���� ��1����2������C��D���˶��ٶ�֪BD=2PC��������֪����PD=2AC���PB=2AP���ɴ����AP��ֵ��
��3����ϣ�1������2�����н��
��4�������軭��ͼʾ������AQ-BQ=PQ���AQ=PQ+BQ��Ȼ�����AP=BQ���Ӷ����PQ��AB�Ĺ�ϵ��
��� �⣺��1������C��D���˶��ٶ�֪��BD=2��PC=1��
��BD=2PC��
��PD=2AC��
��BD+PD=2��PC+AC������PB=2AP��
��AB=12cm��AB=AP+PB��
��12=3AP����AP=4cm��
��2������C��D���˶��ٶ�֪��BD=4��PC=2��
��BD=2PC��
��PD=2AC��
��BD+PD=2��PC+AC������PB=2AP��
��AB=12cm��AB=AP+PB��
��12=3AP����AP=4cm��
��3������C��D���˶��ٶ�֪��BD=2PC
��PD=2AC��
��BD+PD=2��PC+AC������PB=2AP��
���P���߶�AB�ϵ�$\frac{1}{3}$������AP=4cm��
��4����ͼ��
��AQ-BQ=PQ��
��AQ=PQ+BQ��
�֡�AQ=AP+PQ��
��AP=BQ��
��PQ=$\frac{1}{3}$AB=4cm��
����Q'��AB���ӳ�����ʱ��
AQ��-AP=PQ�䣬
����AQ��-BQ��=PQ=AB=12cm��
����������PQ=4cm��12cm��
���� ���⿼����һԪһ�η��̵�Ӧ�ã������ľ��룬��������߶εĺ͡��������ת���߶�֮���������ϵ��ʮ�ֹؼ���һ�㣮


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
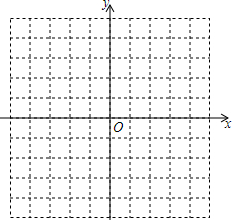 һ�κ���y=kx+4��ͼ���㣨3��-2��
һ�κ���y=kx+4��ͼ���㣨3��-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com