
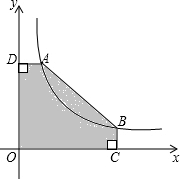
 如图,A(2,m),B(6,n)是双曲线y=
如图,A(2,m),B(6,n)是双曲线y=| 12 |
| x |
| 12 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
 如图所示,在墙角B处有一只猫,通过挂在墙CD上点O处的一平面镜正好看到另一房间A处有一只老鼠在偷吃东西.已知A点和B点均距挂镜子的墙CD=4米,A、B两点距离是6米.若猫去捉老鼠必经过O点处的门口(不计门口宽度),请你猜测猫从B点到A点至少要经过多少米的路程?
如图所示,在墙角B处有一只猫,通过挂在墙CD上点O处的一平面镜正好看到另一房间A处有一只老鼠在偷吃东西.已知A点和B点均距挂镜子的墙CD=4米,A、B两点距离是6米.若猫去捉老鼠必经过O点处的门口(不计门口宽度),请你猜测猫从B点到A点至少要经过多少米的路程?查看答案和解析>>
科目:初中数学 来源: 题型:
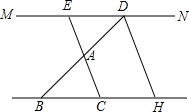 已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.
已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.
如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com