
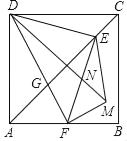
【题目】如图,正方形ABCD中,AD=8,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则(1)FM=_____;(2)tan∠MDE=_____.
【答案】![]()
![]()
【解析】
(1)如图,过E作EP⊥AP,EQ⊥AD,根据正方形的性质得到∠EAQ=∠EAP=45°,推出四边形APEQ是正方形,根据全等三角形的性质得到DE=EF,DQ=FP,且AP=EP,设EP=x,则DQ=8-x=FP=x-4,根据勾股定理得到AE=![]() ,DE=
,DE=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =2,过G作GH⊥AB,过M作MK⊥AB,过M作ML⊥AD,根据勾股定理得到结论;
=2,过G作GH⊥AB,过M作MK⊥AB,过M作ML⊥AD,根据勾股定理得到结论;
(2)推出DM在正方形对角线DB上,过M作MK⊥AB,过N作NI⊥AB,则BK=MK=![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到![]() ,求得FI=4-y=1,于是得到结论.
,求得FI=4-y=1,于是得到结论.
(1)如图,过E作EP⊥AP,EQ⊥AD,
∵四边形APEQ是正方形,
∴DC∥AB,
∴△DGC∽△FGA,
∴![]() =2,
=2,
∵AC=8![]() ,DF=4
,DF=4![]()
∴CG=![]() ,
,
∴EG=![]() =
=![]() ,
,
AG=![]() AC=
AC=![]() ,
,
过G作GH⊥AB,过M作MK⊥AB,过M作ML⊥AD,

则易证△GHF≌△FKM全等,
∴GH=FK=![]() ,HF=MK=
,HF=MK=![]() ,
,
∴FM=![]() ;
;
∵ML=AK=AF+FK=4+![]() =
=![]() ,DL=AD-MK=8-
,DL=AD-MK=8-![]() =
=![]() ,
,
即DL=LM,
∴∠LDM=45°
∴DM在正方形对角线DB上,
过N作NI⊥AB,则NI=IB,
设NI=y,
∵NI∥EP
∴![]() ,
,
∴![]() ,
,
解得y=3,
所以FI=4-y=1,
∴I为FP的中点,
∴N是EF的中点,
∴EN=![]() EF=
EF=![]() ,
,
∵DF=4![]() ,
,
∴DE=2![]() ,
,
∴tan∠MDE=![]() ,
,
故答案为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为________(用含a的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图将小球从斜坡的O点抛出,小球的抛出路线可以用二次函数y=ax2+bx刻画,顶点坐标为(4,8),斜坡可以用y=![]() x刻画.
x刻画.
(1)求二次函数解析式;
(2)若小球的落点是A,求点A的坐标;
(3)求小球飞行过程中离坡面的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0两根为x1,x2,x2+x1=﹣![]() ,x2.x1=
,x2.x1=![]() .如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为( )
.如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为( )
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
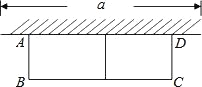
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在成都地铁6号线某站通道的建设中,建设工人将坡长为10米(AB=10米),坡角60°(∠BAE=60°)的斜坡通道改造成坡角为45°(∠BDE=45°)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求截面图上AD的长.(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
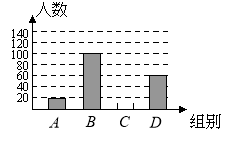
A组:![]() ;B组:
;B组:![]()
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小清为班级办黑板报时遇到一个难题,在版面设计过程中需要将一个半圆三等分,小华帮他设计了一个尺规作图的方法.
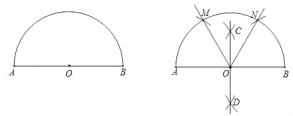
小华的作法如下:
(1)作AB的垂直平分线CD交AB于点O;
(2)分别,以A、B为圆心,以AO(或BO)的长为半径画弧,分别交半圆于点M、N;
(3)连接OM、ON即可
请根据该同学的作图方法完成以下推理:
∵半圆AB
∴ 是直径.
∵CD是线段AB的垂直平分线
∴OA=OB(依据: )
∵OA=OM=
∴△OAM为等边三角形(依据: )
∴∠AOM=60°(依据: )
同理可得∠BON=60°
∠AOM=∠BON=∠MON=60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com