
【题目】如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(2,1).直线OM是一次函数y=-x的图象.将直线OM沿x轴正方向平行移动.
(1)填空:直线OM与x轴所夹的锐角度数为 °;
(2)求出运动过程中⊙A与直线OM相切时的直线OM的函数关系式;(可直接用(1)中的结论)
(3)运动过程中,当⊙A与直线OM相交所得的弦对的圆心角为90°时,直线OM的函数关系式.

【答案】(1)45;(2) y=-x+3-![]() 或y=-x+3+
或y=-x+3+![]() ;(3) y=-x+2或y=-x+4.
;(3) y=-x+2或y=-x+4.
【解析】
(1)利用直线y=x上点的坐标特征易得直线y=x为第二、三四象限的角平分线,则直线OM与x轴所夹的锐角度数为45°;
(2)如图1中,设⊙A与x轴相切于点C,平移后的直线OM与⊙A相切于点E,交x轴于P,连接AE,AC,作ED⊥AC于D.求出点E坐标,利用待定系数法即可解决问题,再根据对称性解决另一种相切情形;
(3)当平移后的直线OM经过点C(⊙A与x轴的切点)时,弦EC所对的圆心角为90°,此时直线EC的解析式为y=x+2.再根据对称性解决另一种情形.
解:(1)∵直线y=-x上点到x轴和y轴的距离相等,
∴直线y=x为第二、四象限的角平分线,
∴直线OM与x轴所夹的锐角度数为45°;
故答案为45.
(2)如图1中,设⊙A与x轴相切于点C,平移后的直线OM与⊙A相切于点E,交x轴于P,连接AE,AC,作ED⊥AC于D.
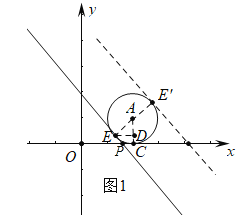
∵∠OPE=45°,
∴∠EPC=135°,
∵∠AEP=∠ACP=90°,
∴∠EAD=45°,
∵AE=1,
∴AD=DE=![]()
∴CD=1-![]()
∴E(2-![]() ,1-
,1-![]() ),
),
设直线PE的解析式为y=-x+b,
则有1-![]() =-(2-
=-(2-![]() )+b,
)+b,
∴b=3-![]() ,
,
∴平移后直线OM的解析式为y=-x+3-![]() .
.
根据对称性可知,直线PE向右平移![]() 个单位直线与⊙A相切于点E′,此时直线OM的解析式为y=-x+3+
个单位直线与⊙A相切于点E′,此时直线OM的解析式为y=-x+3+![]() .
.
综上所述,运动过程中⊙A与直线OM相切时的直线OM的函数关系式为y=-x+3-![]() 或y=-x+3+
或y=-x+3+![]() .
.
(3)当平移后的直线OM经过点C(⊙A与x轴的切点)时,弦EC所对的圆心角为90°,此时直线EC的解析式为y=-x+2.
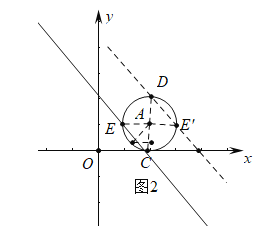
根据对称性可知,当直线EC继续向右平移2个单位,与⊙A交于点D,E′,此时∠DAE′=90°,此时直线的解析式为y=-x+4.
综上所述,满足条件的直线OM的解析式为:y=-x+2或y=-x+4.


科目:初中数学 来源: 题型:
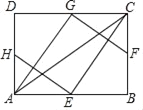
【题目】如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=![]() ,则AB的长为__________.
,则AB的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
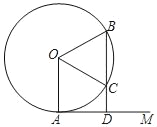
【题目】已知:如图,AM为⊙O的切线,A为切点.过⊙O上一点B作BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB.
(1)求∠AOB的度数;
(2)当⊙O的半径为4cm时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ECD都是等边三角形,△EBC可以看作是△DAC经过平移、轴对称或旋转得到.
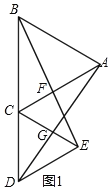
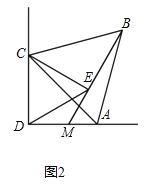
(1)如图1,当B,C,D在同一直线上,AC交BE于点F,AD交CE于点G,求证:CF=CG;
(2)如图2,当△ABC绕点C旋转至AD⊥CD时,连接BE并延长交AD于M,求证:MD=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
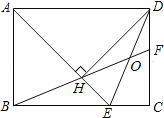
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有_____.
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
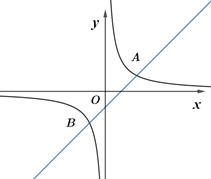
【题目】如图,直线y=x+m与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组直接写出点B的坐标;
(3)直线y=﹣2x+4m经过点B吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织七、八、九年级学生参加全区作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.

(1)此次参赛的作文篇数共有 篇;
(2)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(3)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com