
【题目】如图,在平面直角坐标系中,直线y=-2x+2与x轴交于点B,与y轴交于点A,抛物线y=-![]() x2+bx+c与线段AB交于点E,并经过原点O,且点E的横坐标为
x2+bx+c与线段AB交于点E,并经过原点O,且点E的横坐标为![]() .
.
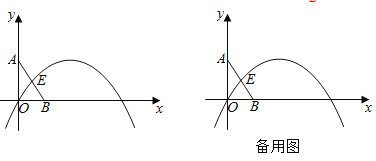
(1)求抛物线的表达式;
(2)在抛物线上是否存在点C,使得以AC为直径的圆恰好经过点B,若存在,求出所有满足条件的点C的坐标,若不存在,请说明理由;
(3)若D是第(2)小题中圆上的动点,直线y=![]() x+m经过点D,求m的取值范围.
x+m经过点D,求m的取值范围.
【答案】(1)y=![]() ;(2)点C(3,1)或
;(2)点C(3,1)或![]() ;(3)
;(3)![]() ≤m≤
≤m≤![]() 或
或![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点E的坐标,由点O,E的坐标利用待定系数法即可求出抛物线的表达式;
(2)利用一次函数图象上点的坐标特征可求出点A,B的坐标,过点B作BC⊥AB,交抛物线于点C,交y轴于点F,则△AOB∽△BOF,利用相似三角形的性质可求出点F的坐标,由点B,F的坐标利用待定系数法可求出直线BC的表达式,联立直线BC与抛物线的表达式成方程组,通过解方程组可求出点C的坐标;
(3)设线段AC1的中点为M,过点M作D1D2∥AB交⊙M于点D1,D2,过点D1作D1P1∥BC交y轴于点P1,过点D2作D2P2∥BC交y轴于点P2,过点M作MN∥BC交y轴于点N,过点P1作P1P3⊥D2P2于点P3,则四边形D1P1P3D2为矩形,△OAB∽△P3P1P2,由点A,C1的坐标可得出点M的坐标及AC1的长度,结合直线BC的表达式可求出直线MN的表达式,利用一次函数图象上点的坐标特征可求出点N的坐标,由△OAB∽△P3P1P2利用相似三角形的性质可得出P1P2的长度,由点M为线段D1D2的中点可得出点N为线段P1P2的中点,结合点N的坐标及P1P2的长度可得出点P1,P2的坐标,进而可得出m的取值范围.
(1)∵ 直线y=-2x+2经过点E,点E的横坐标为![]() ,
,
∴当x=![]() 时,y=-2×
时,y=-2×![]() +2=1,
+2=1,
∴点E(![]() ,1),
,1),
∵ 抛物线y=-![]() x2+bx+c与线段AB交于点E,并经过原点O,
x2+bx+c与线段AB交于点E,并经过原点O,
∴c=0,
∴![]() ,
,
解之:b=![]() ,
,
∴抛物线的解析式为:y=![]() ;
;
(2)∵ 直线y=-2x+2与x轴交于点B,与y轴交于点A,
当x=0时,y=2,
∴点A(0,2),
当y=0时,-2x+2=0,
解之:x=1,
∴点B(1,0),
∵ 以AC为直径的圆恰好经过点B,
∴AB⊥BC,
∴KAB·KBC=-1,
∵ yAB=-2x+2,
设BC的函数解析式为:yBC=![]() , 将点B代入得
, 将点B代入得![]() ,
,
解之:b=![]() ,
,
∴yBC=![]() ,
,
解方程组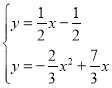 ,得
,得![]() 或
或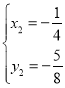 ,
,
∴点C(3,1)或![]() ;
;
(3)∵点A(0,2),C(3,1),AC是直径,
∴圆心O的坐标为:![]() ,
,
当直线![]() 与圆O1相切于点M时,
与圆O1相切于点M时,
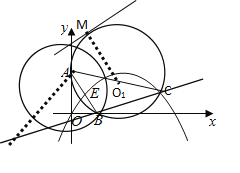
∴![]() ,
,
∴![]() ,
,
解之:x=![]() ,
,
∴点M(![]() ,
, ![]() )
)
∴r=O1M=![]() ,
,
∴![]() ,
,
整理得:16m2-24m-41=0,
解之:m1=![]() , m2=
, m2=![]() ,
,
∴![]() ≤m≤
≤m≤![]() ,
,
同理可得![]() ,
,
∴![]() ≤m≤
≤m≤![]() 或
或![]()


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】吴江区某桶装水经营部每天的房租、人员工资等固定成本为150元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量![]() (桶)与销售单价
(桶)与销售单价![]() (元)的函数图象如图所示.
(元)的函数图象如图所示.
(1)求日均销售量![]() (桶)与销售单价
(桶)与销售单价![]() (元)的函数关系;
(元)的函数关系;
(2)若该经营部希望日均获利1200元,求该桶装水的销售单价.

查看答案和解析>>
科目:初中数学 来源: 题型:
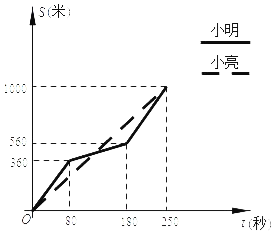
【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次男子1000米耐力测试中,小明和小亮同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示:
(1)当80≤t≤180时,求小明所跑的路程S(米)与所用的时间t(秒)之间的函数表达式;
(2)求他们第一次相遇的时间是起跑后的第几秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
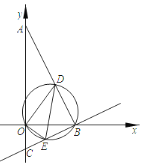
【题目】如图,在平面直角坐标系中,△ABC的顶点在坐标轴上,A,B,C三点的坐标分别为 (0,2),(1,0),(0,-0.5),D为线段AB上-个动点(不与点A,B重合),过B,D,0三点的圆与直线BC交于点E,当△OED面积取得最小值时,ED的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生产某种农产品的成本每千克20元,调查发现,该产品每天销售量y(千克)与销售单价x(元/千克)满足如下关系:![]() ,设这种农产品的销售利润为w元.
,设这种农产品的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)物价部门规定这种产品的销售价不得高于每千克28元,该农户想在这种产品经销季节每天获得150元的利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小如同学设计的“作已知直角三角形的外接圆”的尺规作图过程
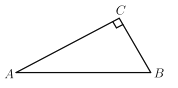
已知:![]() ,
,![]() .
.
求作:![]() 的外接圆.
的外接圆.
作法:如图,
①分别以点![]() 和
和![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点;
两点;
②作直线![]() ,交
,交![]() 于点
于点![]() ;
;
③以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() .
.
![]() 即为所求作的圆.
即为所求作的圆.
根据小如同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹).
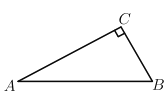
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 由作图,
由作图,![]() ,
,![]() ,
,
![]() 且
且![]() (__________)(填推理的依据).
(__________)(填推理的依据).
![]() ,
,
![]() (__________)(填推理的依据).
(__________)(填推理的依据).
![]() ,
,
![]() ,
,![]() ,
,![]() 三点在以
三点在以![]() 为圆心,
为圆心,![]() 为直径的圆上.
为直径的圆上.
![]() 为
为![]() 的外接圆.
的外接圆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式ax2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
ax2+bx+c | … | 3 |
| ﹣1 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=ax2+bx+c,则当x取何值时,y<0;
(3)当0<x<3,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com