
【题目】如图,在等腰![]() 中,
中,![]() 为
为![]() 延长线上一点,点
延长线上一点,点![]() 在
在![]() 上,且
上,且![]()
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.
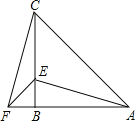
【答案】(1)见解析;(2)30°
【解析】
(1)根据在△ABC中,AB=CB,∠ABC=90°,且AE=CF,根据HL可得到Rt△ABE和Rt△CBF全等;
(2)根据Rt△ABE≌Rt△CBF,可得出∠EAB=∠BCF,再根据∠BCA=∠BAC=45°,∠ACF=60°,可以得到∠CAE的度数.
(1)证明:∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)解:∵AB=CB,∠ABC=90°,∠ACF=60°,∠ACF=∠BCF+∠BCA,
∴∠BCA=∠BAC=45°,
∴∠BCF=15°,
∵Rt△ABE≌Rt△CBF,
∴∠EAB=∠BCF=15°,
∴∠CAE=∠BAC-∠EAB=45°-15°=30°.


科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡顶![]() 处的同一水平面上有一座古塔
处的同一水平面上有一座古塔![]() ,数学兴趣小组的同学在斜坡底
,数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求古塔
.求古塔![]() 的高度.(结果精确到
的高度.(结果精确到![]() 米,参考数据:
米,参考数据: ![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
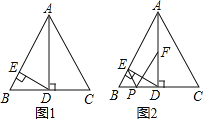
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=![]() ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图![]() 为她们剌绣最简单的四个图案,这些图案都是由小正方形构成的,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),研究发现第
为她们剌绣最简单的四个图案,这些图案都是由小正方形构成的,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),研究发现第![]() 个图案中共有
个图案中共有![]() 个;小正方形.(
个;小正方形.(![]() 为整数,且
为整数,且![]() )
)
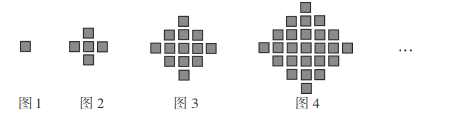
(1)请写出第![]() 个图案中有____个小正方形;
个图案中有____个小正方形;
(2)猜想第![]() 个图案和第
个图案和第![]() 个图案中小正方形个数之差为
个图案中小正方形个数之差为
(3)证明(2)中的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋里装着白、红、黑三种颜色的小球(除颜色外形状大小完全相同),其中白球3个、红球2个、黑球1个.
(1)随机从袋中取出一个球,求取出的球是黑球的概率;
(2)若取出的第一只球是红球,不将它放回袋里,从袋中余下的球中再随机地取出1个,这时取出的球是黑球的概率是多少?
(3)若取出一个球,将它放回袋中,从袋中再随机地取出一个球,两次取出的球都是白球的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在右边的平面直角坐标系中描出以下三点:![]() 、
、![]() 、
、![]() 并回答如下问题:
并回答如下问题:
![]() 在平面直角坐标系中画出△ABC;
在平面直角坐标系中画出△ABC;
![]() 在平面直角坐标系中画出△A′B′C′;使它与
在平面直角坐标系中画出△A′B′C′;使它与![]() 关于x轴对称,并写出点C′的坐标______;
关于x轴对称,并写出点C′的坐标______;
![]() 判断△ABC的形状,并说明理由.
判断△ABC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数 y=ax2+bx﹣(a+b)(a,b 是常数,a≠0).
(1)判断该二次函数图象与 x 轴的交点的个数,说明理由.
(2)若该二次函数图象经过 A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式.
(3)若 a+b<0,点 P(2,m)(m>0)在该二次函数图象上,求证:a>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4的图象分别与x轴、y轴交于点A,B.
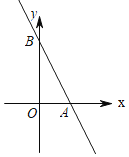
(1)求△AOB的面积;
(2)在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com