
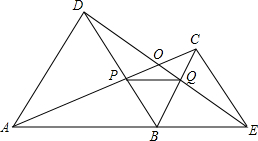
 已知△ABD和△BCE均为等边三角形,连接AC,DE交DB于点P,交DE于点O,你能得到哪些结论,并给予证明.
已知△ABD和△BCE均为等边三角形,连接AC,DE交DB于点P,交DE于点O,你能得到哪些结论,并给予证明.
|

|


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
 (1)已知线段a,b.用圆规和直尺作线段AC,及线段AC上的点B,使AC=2a+b,其中AB=2a,BC=b.(不写作法但保留作图痕迹);
(1)已知线段a,b.用圆规和直尺作线段AC,及线段AC上的点B,使AC=2a+b,其中AB=2a,BC=b.(不写作法但保留作图痕迹);查看答案和解析>>
科目:初中数学 来源: 题型:
 某小区有一块长方形草坪,为方便居民穿行和健身,小区管理人员沿草坪对角线修一条长39m的砖路,并在草坪周围铺设了一圈石子路(石子路的宽度忽略不计),如图所示,已知长方形草坪的长与宽之比为3:2,求所铺设的石子路的总长度.(结果精确到0.1,参考数据:
某小区有一块长方形草坪,为方便居民穿行和健身,小区管理人员沿草坪对角线修一条长39m的砖路,并在草坪周围铺设了一圈石子路(石子路的宽度忽略不计),如图所示,已知长方形草坪的长与宽之比为3:2,求所铺设的石子路的总长度.(结果精确到0.1,参考数据:| 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com