
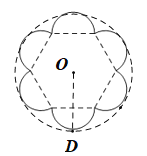
【题目】已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率=![]() ×100%)
×100%)
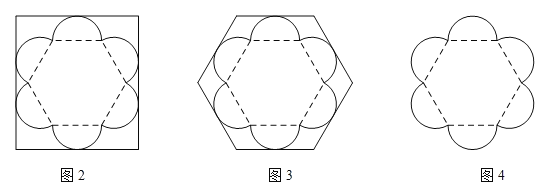
(1)请分别计算出图2与图3中的底面利用率(结果保留到0.1%);
(2)考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
【答案】(1)图2、3的底面利用率分别约为66.4%、40.2%;(2)设计底面为圆形的包装盒,利用率约为84.5%.
【解析】
(1)设半圆直径与正六边形的边长为a,根据正多边形和圆的知识,算出月饼面积,再算出图2正方形的边长,即可求出图2的面积,和图2底面的利用率;图3的包装盒六边形和月饼相似,利用面积比等于相似比的平方,求出图3包装盒的底面利用率;
(2)设计底面为圆形的包装盒,求出其半径、面积、底面利用率,满足底面利用率不低于80%.
解:(1)设半圆直径与正六边形的边长![]() a,连接正六边形的中心
a,连接正六边形的中心![]() 和两相邻的顶点
和两相邻的顶点![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() =a,
=a,
过点![]() 作
作![]() ,
,
∴![]() ,
,![]()
![]() ,
,
∴![]()
![]() =
=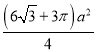 ,
,
延长OC与其中一个半圆交于点D,
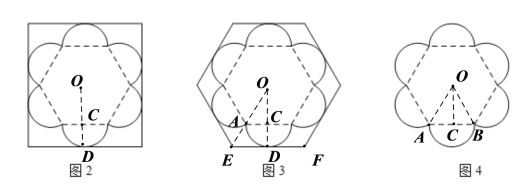
则![]()
![]()
 ,
,
∴![]()
![]() ,
,
![]()
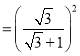
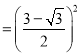
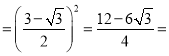
![]()
![]() 40.2%;
40.2%;
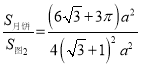 =
=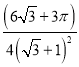 =
=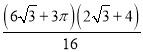 =
=![]()
![]() 66.4%;
66.4%;
答:图2、3的底面利用率分别约为66.4%、40.2%;
(2)商家的要求是否能够满足,设计如图所示底面为圆的包装盒,半径为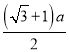 ,
,
![]()
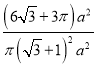 =
=
![]()
![]() ,
,
答:设计底面为圆形的包装盒,利用率约为84.5%.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y ax2 2ax 3a2 3(其中x是自变量),当x 2时,y随x的增大而增大,且3 x 0时,y的最大值为9,则a的值为( ).
A.1或![]() B.
B.![]() 或
或![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某交为了开展“阳光体育运动”,计划购买篮球和足球,已知足球的单价比篮球的单价多![]() 元.若购买
元.若购买![]() 个篮球和
个篮球和![]() 个足球需花费
个足球需花费![]() 元.
元.
(1)求篮球和足球的单价各是多少元;
(2)若学校购买篮球和足球共![]() 个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈市某高新企业制定工龄工资标准时充分考虑员工对企业发展的贡献,同时提高员工的积极性、控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案.
Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄-18,
企业工龄=现年年龄-参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
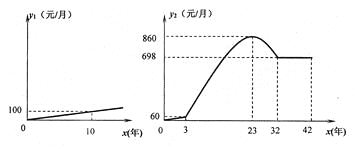
(1)求出y1、y2与工龄x之间的函数关系式;
(2)现年28岁的高级技工小张从18岁起一直在深圳实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?
(3)已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
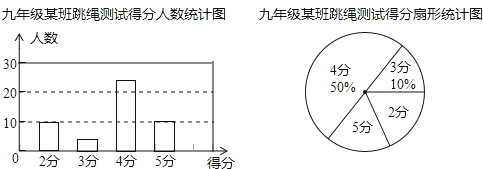
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 是射线
是射线![]() 上一个动点(不与点
上一个动点(不与点![]() 、
、![]() 重合),联结
重合),联结![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
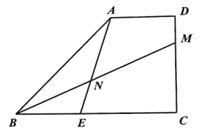
(1)求![]() 的长;
的长;
(2)当动点![]() 在线段
在线段![]() 上时,试求
上时,试求![]() 与
与![]() 之间的函数解析式,并写出函数的定义域;
之间的函数解析式,并写出函数的定义域;
(3)当动点![]() 运动时,直线
运动时,直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() ,请直接写出这时线段
,请直接写出这时线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
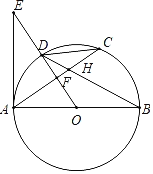
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D是![]() 的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)求证:AE是⊙O的切线;
(2)若DH=9,tanC=![]() ,求直径AB的长.
,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则sin∠CAD的值为( )
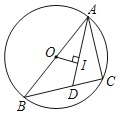
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com