
分析 将原式变形为x+$\frac{9}{x}$,根据该老师的方法,可在面积为9的矩形中寻找,按其方法可一步步得出结论等于6.
解答 解:原式=x+$\frac{9}{x}$.
在面积是9的矩形中,设矩形的一边长为x,则另一边长是$\frac{9}{x}$,矩形的周长是2(x+$\frac{9}{x}$),
当矩形成为正方形时,就有x=$\frac{9}{x}$(x>0),
解得x=3,
这时矩形的周长2(x+$\frac{9}{x}$)=12最小,
因此x+$\frac{9}{x}$(x>0)的最小值是6.
故答案为:6.
点评 本题考查分式方程的应用,解题的关键是读懂题意,将该老师矩形面积换为9,即可求得结论.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,AF、DE相交于点G,BF、CE相交于点H.求证:四边形EHFG是平行四边形.
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,AF、DE相交于点G,BF、CE相交于点H.求证:四边形EHFG是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
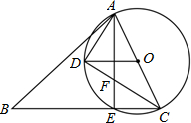 如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系:
某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一直动点A在函数$y=\frac{4}{x}(x>0)$的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交于x轴于点P、Q,当$\frac{QE}{DP}=\frac{4}{9}$时,图中阴影部分的面积等于$\frac{13}{3}$.
如图,一直动点A在函数$y=\frac{4}{x}(x>0)$的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交于x轴于点P、Q,当$\frac{QE}{DP}=\frac{4}{9}$时,图中阴影部分的面积等于$\frac{13}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2(x-2)+n经过原点,与双曲线$y=\frac{n}{x}$相交与点A、B,过点A作AC垂直于x轴,过点B作BC垂直于y轴,AC与BC相交于点C.求:
如图,直线y=2(x-2)+n经过原点,与双曲线$y=\frac{n}{x}$相交与点A、B,过点A作AC垂直于x轴,过点B作BC垂直于y轴,AC与BC相交于点C.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com