
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(4)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)方程整理得:$\frac{2x+11}{(x+2)(x+9)}$=$\frac{2x+11}{(x+3)(x+8)}$,
当2x+11=0,即x=-$\frac{11}{2}$时,方程成立;
当2x+11≠0,即x≠-$\frac{11}{2}$时,则有$\frac{1}{(x+2)(x+9)}$=$\frac{1}{(x+3)(x+8)}$,
去分母整理得:18=24,无解,
经检验x=-$\frac{11}{2}$是分式方程的;
(2)方程整理得:$\frac{1}{x-2005}$+$\frac{1}{x-2009}$=$\frac{1}{x-2008}$+$\frac{1}{x-2006}$,
即$\frac{2x-4014}{(x-2005)(x-2009)}$=$\frac{2x-4014}{(x-2008)(x-2006)}$,
当2x-4014=0,即x=2007时,方程成立;
当2x-4014≠0,即x≠2007时,方程整理得:x2-4014x+2005×2009=x2-4014x+2008×2006,无解,
经检验x=2007是分式方程的解;
(3)方程整理得:$\frac{1}{a}$-$\frac{1}{b}$=$\frac{b}{x}$-$\frac{a}{x}$,
即$\frac{b-a}{ab}$=$\frac{b-a}{x}$,
解得:x=ab,
经检验x=ab是分式方程的解;
(4)去分母得:x(x-a)-3(x-1)=x(x-1),
整理得:(a+2)x=3,
解得:x=$\frac{3}{a+2}$,
经检验x=$\frac{3}{a+2}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
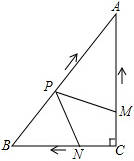 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,分别沿CA,CB向终点A,B移动,点M的速度是每秒1cm,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动.设移动时间为t(0<t<2.5)秒,当t为何值时,以A,P,M为顶点的三角形可能与△BPN相似?此时点N的速度时多少?
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,分别沿CA,CB向终点A,B移动,点M的速度是每秒1cm,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动.设移动时间为t(0<t<2.5)秒,当t为何值时,以A,P,M为顶点的三角形可能与△BPN相似?此时点N的速度时多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com