
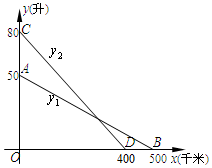
 如图,线段AB、CD分别是一辆轿车的油箱剩余油量y1(升)与另一辆客车的油箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.
如图,线段AB、CD分别是一辆轿车的油箱剩余油量y1(升)与另一辆客车的油箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.分析 (1)设出线段AB、CD所表示的函数解析式,由待定系数法结合图形可得出结论;
(2)由(1)的结论算出当油箱的剩余油量相同时,跑的路程数,再由时间=路程÷速度,即可得出结论.
解答 解:(1)设AB、CD所表示的函数解析式分别为y1=k1x+50,y2=k2x+80.
结合图形可知:$\left\{\begin{array}{l}{0=500{k}_{1}+50}\\{0=400{k}_{2}+80}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-0.1}\\{{k}_{2}=-0.2}\end{array}\right.$.
故y1=-0.1x+50(0≤x≤500),y2=-0.2x+80(0≤x≤400).
(2)令y1=y2,则有-0.1x+50=-0.2x+80,
解得:x=300.
轿车行驶的时间为300÷100=3(小时);
客车行驶的时间为300÷80=$3\frac{3}{4}$(小时),
$3\frac{3}{4}$-3=$\frac{3}{4}$小时=45(分钟).
答:当油箱的剩余油量相同时,两车行驶的时间相差45分钟.
点评 本题考查了一次函数的应用,解题的关键:(1)熟练运用待定系数法就解析式;(2)找出剩余油量相同时行驶的距离.本题属于基础题,难度不大,解决该类问题应结合图形,理解图形中点的坐标代表的意义.


科目:初中数学 来源: 题型:填空题
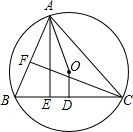 如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).
如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 长 | 宽 | 高 | |
| 小纸盒 | a | b | c |
| 大纸盒 | 3a | 2b | 2c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
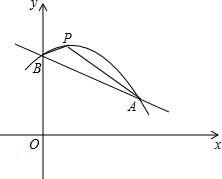 如图,已知抛物线y=-$\frac{1}{8}$x2+bx+c与一次函数y=-$\frac{1}{2}$x+6的图象交于A(8,m)和y轴上的同一点B,P是抛物线的顶点.
如图,已知抛物线y=-$\frac{1}{8}$x2+bx+c与一次函数y=-$\frac{1}{2}$x+6的图象交于A(8,m)和y轴上的同一点B,P是抛物线的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com