
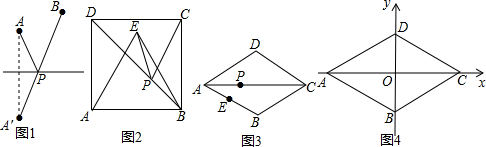
���� ��1�����������ε����ʣ���C����BD�ĶԳƵ�Ϊ��A��������Գ�-�������֪ʶ��֪����AEΪPC+PE����Сֵ��
��2���������ε����ʣ���B����AC�ĶԳƵ�Ϊ��D��������Գ�-�������֪ʶ��֪����DEΪPB+PE����Сֵ��������֪���������DE���ɣ�
��3�����������֪����PB��ABʱ����P������̵�ʱ���ڵ����B���������M�����꼴�ɣ�
��� �⣺��1�����������ε����ʿ�֪��
��C����BD�ĶԳƵ�Ϊ��A��
��PC+PE�ĺ���СֵΪAE��
��������ABCD�����Ϊ16����AB=4��
�ߡ�ABE�ǵȱ������Σ���AE=4��
��PC+PE�ĺ���СֵΪ4��
��2���������ε����ʿ�֪��
��B����AC�ĶԳƵ�Ϊ��D��
��DEΪPB+PE����Сֵ��
�ߡ�B=120�㣬���BAD=60�㣬
���ABD�ǵȱ������Σ�
��E��AB���е㣬����DE��AB��
��AB=2����AE=$\sqrt{3}$��
��PB+PE����Сֵ��$\sqrt{3}$��
��3��ʹ��P������̵�ʱ���ڵ����B����
�൱PB��ABʱ���������⣬
�ߡ�DAB=60�㣬���BAC=30�㣬��AB=6��
��BM=2$\sqrt{3}$��
�ߡ�OBM=30�㣬BM=2$\sqrt{3}$��
��OM=$\sqrt{3}$��
���M��������$\sqrt{3}$��0��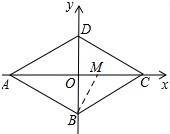
���� ���⿼������ı���֪ʶ���ۺ����ã����������Գ�-��������ǽ���Ĺؼ���ע�⣺�����κ����εĶԽ��ߴ�ֱ�һ���ƽ�֣��������κ����β����ڵ����������һ���Խ�����Գƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
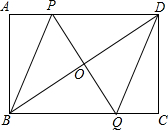 ��ͼ������ABCD�У���P���߶�AD�ϵ�һ�����㣬OΪBD���е㣬PO���ӳ��߽�BC��Q��
��ͼ������ABCD�У���P���߶�AD�ϵ�һ�����㣬OΪBD���е㣬PO���ӳ��߽�BC��Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
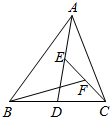 ��ͼ���ڡ�ABC�У���D��E��F�ֱ�ΪBC��AD��CE���е㣮��S��BFC=1����S��ABC=4��
��ͼ���ڡ�ABC�У���D��E��F�ֱ�ΪBC��AD��CE���е㣮��S��BFC=1����S��ABC=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{3}$ | B�� | $\sqrt{40}$=5$\sqrt{8}$ | C�� | $\sqrt{\frac{8}{9}}$=$\frac{4\sqrt{2}}{3}$ | D�� | 8$\sqrt{\frac{3}{2}}$=4$\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
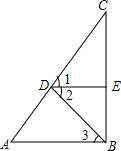 ��ͼ����1=��2��DE��BC��AB��BC����֤����A=��3��
��ͼ����1=��2��DE��BC��AB��BC����֤����A=��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��k��0����ͼ��A��0��-2����B��1��0�����㣬�뷴��������$y=\frac{m}{x}$��m��0����ͼ���ڵ�һ�����ڽ��ڵ�M������OBM�������2��
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��k��0����ͼ��A��0��-2����B��1��0�����㣬�뷴��������$y=\frac{m}{x}$��m��0����ͼ���ڵ�һ�����ڽ��ڵ�M������OBM�������2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com