
【题目】在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4),抛物线y=-2x2+bx+c经过A、C两点,与x轴的另一个交点为点D.

(1)如图1,求抛物线的函数表达式;
(2)如图2,连接AC、AD,将△ABC沿AC折叠后与AD、y轴分别交于点交于E、G,求OG的长度;
(3)如图3,将抛物线在AC上方的图象沿AC折叠后与y轴交与点F,求点F的坐标.
【答案】(1)y=-2x2+2x+4;(2)![]() ;(3)F(0,
;(3)F(0,![]() ).
).
【解析】
(1)先根据四边形ABCD是矩形得出点A.C坐标,再代入解析式求出b.c的值,从而得出答案;
(2)由△ABC≌△AB′C知∠BCA=∠B′CA.由AO∥BC知∠BCA=∠B′CA,∠BCA=∠OAC,从而得∠B′CA=∠OAC.据此知AG=CG.设OG=x,则AG=CG=4-x.在Rt△OGC中,利用勾股定理可以求得x的值;
(3)在AC上方的抛物线图象取点F的对称点F′,过点F′作y轴的平行线交直线AC于点G,先证F′A=F′G,继而得直线AC的解析式为y=-2x+4,设点F(n,-2n2+2n+4),则G(n,-2n+4).根据F′A2=F′G2求出n的值,从而得出![]() ,F′A=F′G=FA=
,F′A=F′G=FA=![]() ,从而得出点F的坐标.
,从而得出点F的坐标.
解:(1)如图1,

∵四边形OABC是矩形,B(2,4),
∴A(0,4),C(2,0),
∵抛物线y=-2x2+bx+c经过A.C两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线的函数表达式为:y=-2x2+2x+4;
(2)如图2,
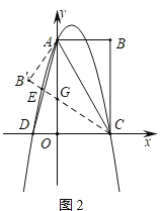
由题意得:△ABC≌△AB′C.
∴∠BCA=∠B′CA.
∵AO∥BC,
∴∠BCA=∠B′CA,∠BCA=∠OAC,
∴∠B′CA=∠OAC.
∴AG=CG.
设OG=x,则AG=CG=4-x.
在Rt△OGC中,22+x2=(4-x)2,
得![]() ,
,
∴![]() ;
;
(3)如图3,在AC上方的抛物线图象取点F的对称点F′,过点F′作y轴的平行线交直线AC于点G.
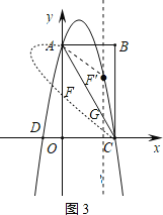
由题意得:∠FAC=∠F′AC,F′A=FA.
∵AO∥F′G,
∴∠FAC=∠AGF′.
∵∠FAC=∠F′AC,∠FAC=∠AGF′.
∴∠F′AC=∠AGF′,
∴F′A=F′G.
设直线AC的解析式为y=kx+b,
把A(0,4),C(2,0)代入得![]() ,解得
,解得![]()
∴直线AC的解析式为:y=-2x+4.
设点F(n,-2n2+2n+4),则G(n,-2n+4).
∴F′G=-2n2+4n,F′A2=n2+(-2n2+2n)2.
∵F′A=F′G.
∴F′A2=F′G2.
即:n2+(-2n2+4n)2=(-2n2+2n)2,
解得:n1=0(舍去),![]() .
.
∴![]() .
.
∴F′A=F′G=FA=![]() ,
,
∴F(0,![]() ).
).


科目:初中数学 来源: 题型:
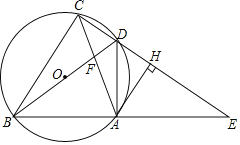
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
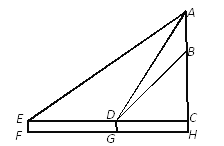
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某校就“经典咏流传”的喜爱情况进行了随机调查.对收集的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据所提供的信息解答:
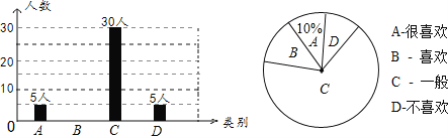
(1)扇形统计图中C部分所对应的扇形圆心角的度数为______,补全条形统计图;
(2)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在北部湾经济区农业示范基地采购A,B两种农产品,已知A种农产品每千克的进价比B种多2元,且用24000元购买A种农产品的数量(按重量计)与用18000元购买B种农产品的数量(按重量计)相同.
(1)求A,B两种农产品每千克的进价分别是多少元?
(2)该公司计划购进A,B两种农产品共40吨,并运往异地销售,运费为500元/吨,已知A种农产品售价为15元/kg,B种农产品售价为12元/kg,其中A种农产品至少购进15吨且不超过B种农产品的数量,问该公司应如何采购才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
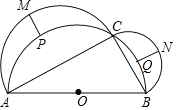
A.17B.18C.19D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数![]() 的图象相交于点A(﹣4,2),B(n,﹣4)
的图象相交于点A(﹣4,2),B(n,﹣4)
(1)求一次函数和反比例函数的表达式;
(2)观察图象,直接写出不等式y1<y2的解集.
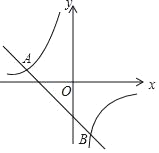
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,且过点(﹣3,0),(1,0),下列说法错误的是( )

A.2a﹣b=0
B.4a﹣2b+c<0
C.(﹣4,y1),(2,y2)是抛物线上两点,则y1>y2
D.y<0时,﹣3<x<1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com