
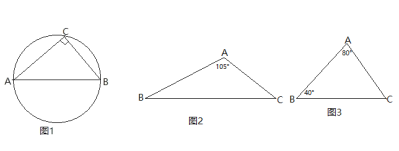
����Ŀ��[̽������]������״Ϊֱ�������ε�ֽƬ��С��ͬѧ����Щ��С��ͬ��Բ��ֽƬȥ��������������ֽƬ��������β������֣���ͼ1,��б��ABΪֱ����Բ���պ��ǿ���Rt��ABC���ǵ������С��Բ����֮Ϊ��С����Բ.
[����Ӧ��]
����Ҳ������һЩ��С��ͬ��Բ������������κͶ۽������Σ�����ͨ������̽�������������
(1)��ͼ2.��![]() �У���A=105��������ֱ�ߺ�Բ��������������ε���С����Բ(��д������������ͼ�ۼ�).
�У���A=105��������ֱ�ߺ�Բ��������������ε���С����Բ(��д������������ͼ�ۼ�).
��2����ͼ3,��![]() �У���A=80������B=40����AB=
�У���A=80������B=40����AB=![]() ���������ABC����С����Բ�İ뾶
���������ABC����С����Բ�İ뾶
[��չ����]
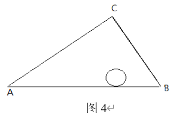
��3����ͼ4,��![]() �У���֪AB=15��AC=12,BC=9���뾶Ϊ1��
�У���֪AB=15��AC=12,BC=9���뾶Ϊ1��![]() ��
��![]() ���ڲ������˶�����
���ڲ������˶�����![]() ���Dz����������
���Dz����������
���𰸡���1������������2��r=2����3��![]() .
.
��������
��1�������⣬��������ε���С����Բ���������ε����Բ.���������Բ��Բ����ÿ���ߵĴ�ֱƽ�����ϣ����������ε�������ֱƽ���߱ؽ���һ�㣬��ֻ���������ߵĴ�ֱƽ���ߣ��佻�㼴ΪԲ��O������OC����OCΪ�뾶����ͼ�������������ɣ�
��2����ͼ������������![]() ����С����ԲΪ
����С����ԲΪ![]() �����Բ������֪�����ɵ�
�����Բ������֪�����ɵ�![]() ����Բ�Ľ�
����Բ�Ľ�![]() ������OA��OB����O��
������OA��OB����O��![]() ���ɵ��������ε����ʿɵ�
���ɵ��������ε����ʿɵ�![]() ����
����![]() �����ù��ɶ�����⼴�ɣ�
�����ù��ɶ�����⼴�ɣ�
��3������֪������![]() ��ֱ�������Σ�����
��ֱ�������Σ�����![]() �������ȥԲ��������ɵ�.
�������ȥԲ��������ɵ�.
��1�������⣬��������ε���С����Բ���������ε����Բ.���������Բ��Բ����ÿ���ߵĴ�ֱƽ�����ϣ����������ε�������ֱƽ���߱ؽ���һ�㣬��ֻ���������ߵĴ�ֱƽ���ߣ��佻�㼴ΪԲ��O������OC����OCΪ�뾶����ͼ���£�
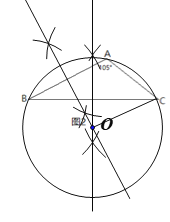
��2����ͼ��![]() ����С����ԲΪ
����С����ԲΪ![]() �����Բ
�����Բ
����OA��OB����O��![]()
![]()
![]()
![]() ��Բ�ܽǶ�����
��Բ�ܽǶ�����
![]() ����
����![]() �ǵ���������
�ǵ���������
![]()
��![]() ��
�У�![]()
�ɹ��ɶ����ã�![]()
��ã�![]()
��![]() ����С����Բ�İ뾶Ϊ2��
����С����Բ�İ뾶Ϊ2��
��3��![]()
![]()
![]() ��ֱ��������
��ֱ��������
![]()
��![]()
����������Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��a��0����ͼ����ͼ��ʾ��
��a��0����ͼ����ͼ��ʾ��
���������
��a��bͬ����
����x=1��x=3ʱ������ֵ�����
��4a+b=0��
����-1��x��5ʱ��y��0��
������ȷ������ ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C����B������Ϊ��3��0��
��x�ύ��A��B���㣬��y�ύ�ڵ�C����B������Ϊ��3��0��
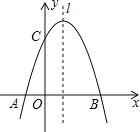
��1����m��ֵ�������ߵĶ������꣮
��2����P�������߶Գ���l�ϵ�һ�����㣬��PA+PC��ֵ��Сʱ�����P�����꣮
��3����M���������ڵ�һ������ͼ���ϵ�����һ�㣬��BCM��������ʱ��M������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��ax��a��y��![]() ��a��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
��a��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
A.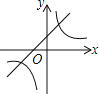 B.
B.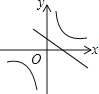
C.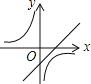 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��24���࣬��1 000��ѧ�������Dzμ���һ����ѧ���ԣ�ѧУͳ��������ѧ���ijɼ����õ�����ͳ��ͼ��

��1�����У���꼶ѧ��������ѧ���Գɼ���ƽ������
��2�����й��ڱ�����ѧ����˵����ȷ���ǣ� ��
A�����꼶ѧ���ɼ���������ƽ�������
B�����꼶ѧ���ɼ�����λ����ƽ�������
C�������ȡһ���࣬�ð�ѧ���ɼ���ƽ�������ھ��꼶ѧ���ɼ���ƽ����
D�������ȡ300��ѧ�������������dzɼ���ƽ�������ƾ��꼶ѧ���ɼ���ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
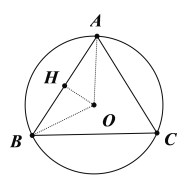
����Ŀ����ͼ������ABC�У�AB=AC��AE�ǽ�ƽ���ߣ�BMƽ�֡�ABC��AE�ڵ�M������B��M����ġ�O��BC�ڵ�G����AB�ڵ�F��FBǡΪ��O��ֱ����
��1���ж�AE���O��λ�ù�ϵ����˵�����ɣ�
��2����BC=6��AC=4CEʱ�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��5��BC��8������ABC���ŵ�B��ת�õ���A��BC������A�Ķ�Ӧ��A������C�Ķ�Ӧ��C��.�����A����BC���ϣ���ô��C�͵�C��֮��ľ���Ϊ____.
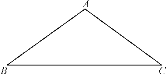
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������Ӱ������ѧУ��˵ĸ߶ȣ�����ijһʱ�̲��1�׳��������ֱ����ʱӰ����1.4�ף���ʱ�����������AB��һ����Ӱ��BD���ڵ����ϣ���һ����Ӱ��CD����¥����ǽ���ϣ��ֱ���BD��11.2�ף�CD��3�ף������AB�ĸ߶�.
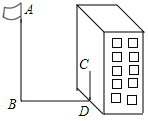
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�ı߳�Ϊ2cm����A=60������M�ӵ�A��������1cm/s���ٶ����B�˶�����N�ӵ�Aͬʱ��������2cm/s���ٶȾ�����D���C�˶���������һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶�������AMN�����y��cm2�����M�˶���ʱ��t��s���ĺ�����ͼ������ǣ�������
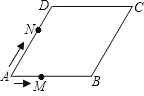
A. 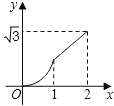 B.
B. 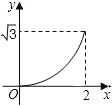
C. 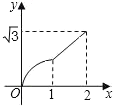 D.
D. 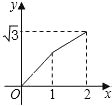
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com