
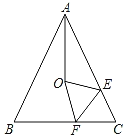
【题目】如图,在等腰△ABC中,AB=AC,把△ABC沿EF折叠,点C的对应点为O,连接AO,使AO平分∠BAC,若∠BAC=∠CFE=50°,则点O是( )
A.△ABC的内心B.△ABC的外心
C.△ABF的内心D.△ABF的外心
【答案】B
【解析】
根据等腰三角形“三线合一”的性质可得AO是BC的垂直平分线,根据垂直平分线的性质可得OB=OC,根据折叠的性质可得CF=OF,∠OFE=∠CFE=50°,进而可求出∠OAC=∠OCA=25°,可得OA=OC,即可得出O是△ABC的外心.
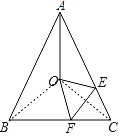
如图,连接OB、OC,
∵AB=AC,AO平分∠BAC,
∴AO是BC的垂直平分线,
∴OB=OC,
∵∠BAC=50°,AO平分∠BAC,
∴∠BAO=∠CAO=25°,
∵把△ABC沿EF折叠,点C的对应点为O,∠CFE=50°,
∴CF=OF,∠OFE=∠CFE=50°,
∴∠OFC=100°,
∴∠FCO=![]() (180°﹣100°)=40°,
(180°﹣100°)=40°,
∵AB=AC,∠BAC=50°,
∴∠ACB=![]() (180°﹣50°)=65°,
(180°﹣50°)=65°,
∴∠OCA=∠ACB﹣∠FCO=65°﹣40°=25°,
∴∠OAC=∠OCA=25°,
∴OA=OC,
∴OA=OB=OC,
∴O是△ABC的外心.
故选:B.


科目:初中数学 来源: 题型:
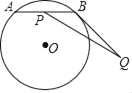
【题目】如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得![]() 的长度是
的长度是![]() ,
,![]() 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
A. 3![]() B. 2
B. 2![]() C. 9 D. 10
C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
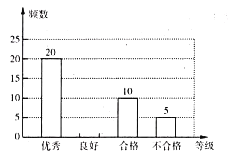
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.
结论1:DM、MN的数量关系是 ;
结论2:DM、MN的位置关系是 ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
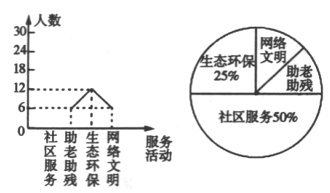
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段y1、y2分别表示小东、小明离B地的距离y1、y2(千米)与所用时间x(小时)的关系.
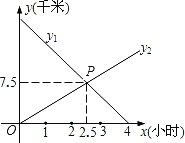
(1)写出y1、y2与x的关系式:______,_______;
(2)试用文字说明:交点P所表示的实际意义.
(3)试求出A、B两地之间的距离.
(4)求出小东、小明相距4千米时出发的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,
上一点,![]() 是
是![]() 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
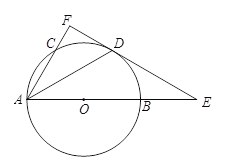
(1)求证:AF⊥EF; (2)若![]() ,AB=5,求线段BE的长.
,AB=5,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个菱形①②③④的较小内角均与已知平行四边形ABCD的∠A相等,边长各不相同.将这四个菱形如图所示放入平行四边形中,未被四个菱形覆盖的部分用阴影表示.若已知两个阴影部分的周长的差,则不需测量就能知道周长的菱形为( )
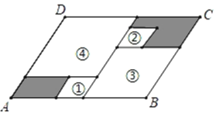
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
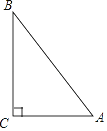
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,点P在边AB上,若△APC为以AC为腰的等腰三角形,则tan∠BCP=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com