
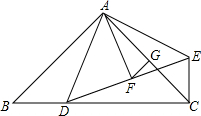
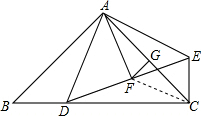
 如图在△ABC中,AB=AC,∠BAC=90°,D是BC上的一点,EC⊥BC,EC=BD
如图在△ABC中,AB=AC,∠BAC=90°,D是BC上的一点,EC⊥BC,EC=BD| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
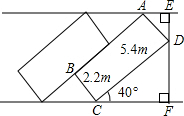 随着人民生活水平的提高,小轿车也逐渐进入千家万户.为了解决停车难问题,我县交警大队在城区划定了许多机动车停车位.如图,矩形ABCD的供一辆机动车停放的车尾示意图,已知BC=2.2m,∠DCF=40°,请计算车位所占街道的宽度EF.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1m)
随着人民生活水平的提高,小轿车也逐渐进入千家万户.为了解决停车难问题,我县交警大队在城区划定了许多机动车停车位.如图,矩形ABCD的供一辆机动车停放的车尾示意图,已知BC=2.2m,∠DCF=40°,请计算车位所占街道的宽度EF.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com