
【题目】如图,已知A、B两点的坐标分别为(4![]() ,0)、(0,4),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的纵坐标为( )
,0)、(0,4),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的纵坐标为( )

A. ![]() +1 B.
+1 B. ![]() -1 C. 2
-1 C. 2![]() +3 D. 2
+3 D. 2![]() +2
+2
【答案】D
【解析】
由P点在第一象限,∠AOP=45°,可设P(a,a).过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,用含a的代数式分别表示PF,CF,在△CFP中由勾股定理求出a的值,即可求得P点的坐标.
解:∵OB=4,OA=4![]() ,
,
∴AB=![]() =8,
=8,
∵∠AOP=45°,
P点横纵坐标相等,可设P(a,a).
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,设为点C,则C(2![]() ,2),
,2),
P点在圆上,P点到圆心的距离为圆的半径4.
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣2,CF=a﹣2![]() ,PC=4,
,PC=4,
∴(a2![]() )2+(a﹣2)2=42,舍去不合适的根,
)2+(a﹣2)2=42,舍去不合适的根,
可得a=2+2![]() ,P(2
,P(2![]() +2,2
+2,2![]() +2);
+2);
即P点坐标为(2![]() +2,2
+2,2![]() +2).
+2).
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在x轴上是否存在点E,使以点B,C,E为顶点的三角形为等腰三角形?如果存在,直接写出E点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
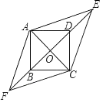
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______ 元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,问四月份比三月份节约用水多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
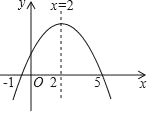
A. ac<0 B. a﹣b+c>0 C. b=﹣4a D. a+b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
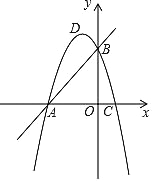
【题目】如图,直线y=x+3与两坐标轴交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)求A、B两点的坐标;
(2)求抛物线的解析式和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,任意两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),规定运算:①A⊕B=(
),规定运算:①A⊕B=(![]() ,
, ![]() );②AB=
);②AB=![]() ;③当
;③当![]() 且
且![]() 时,A=B,有下列四个命题:(1)若A(1,2),B(2,﹣1),则A⊕B=(3,1),AB=0;
时,A=B,有下列四个命题:(1)若A(1,2),B(2,﹣1),则A⊕B=(3,1),AB=0;
(2)若A⊕B=B⊕C,则A=C;
(3)若AB=BC,则A=C;
(4)对任意点A、B、C,均有(A⊕B)⊕C=A⊕(B⊕C)成立,其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com