Question

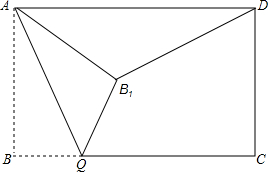
8．如图，长方形ABCD中AB=2，BC=4，点Q是线段BC上一点，连接AQ，作点B关于直线AQ的对称点B，连接AB₁，QB₁．
（1）当B₁落在线段AD上时，BQ=2．
（2）连接B₁D，当△AB₁D为直角三角形时，BQ的4-2$\sqrt{3}$．

Answer 1

分析 （1）当B₁落在线段AD上时，根据点B和点B₁关于AQ对称，得出AB₁=AB，四边形ABQB₁是正方形，即可求出结果；
（2）作∠AQE=∠BAQ=15°，先求出∠BAB₁=30°，设BQ=x，则EQ=2BQ=2x，BE=$\sqrt{3}$x，AE=2x，得出方程：2x+$\sqrt{3}$x=2，解方程即可．

解答 解：（1）当B₁落在线段AD上时，
∵点B和点B₁关于AQ对称，
∴AB₁=AB，四边形ABQB₁是正方形，
∴BQ=AB=2；
故答案为：2；
（2）∵点B和点B₁关于AQ对称，
∴AB₁=AB=2，
∵四边形ABCD是长方形，
∴AD=BC=4=2AB₁，
∵△AB₁D为直角三角形，
∴∠ADB₁=30°，∠DAB₁=60°，
∴∠BAB₁=30°，
∴∠BAQ=$\frac{1}{2}$×30°=15°，
作∠AQE=∠BAQ=15°，如图所示：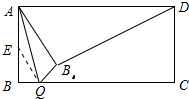
∴∠BEQ=30°，AE=QE，
设BQ=x，则EQ=2BQ=2x，
∴BE=$\sqrt{3}$x，
∴AE=2x，
∴AB=2x+$\sqrt{3}$x，
∴2x+$\sqrt{3}$x=2，
解得：x=4-2$\sqrt{3}$；
故答案为：4-2$\sqrt{3}$．

点评 本题考查了矩形的性质、轴对称的性质以及锐角三角函数；设出未知数根据题意得出方程是解决问题的关键．