
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示,并将测试结果绘制成如下两幅不完整的统计图.
表示,并将测试结果绘制成如下两幅不完整的统计图.
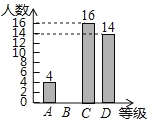
书写能力等级测试条形统计图:
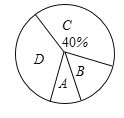
书写能力等级测试扇形统计图:
请根据统计图中的信息解答以下问题:
(1)本次抽取的学生共有______人,扇形统计图中![]() 所对应扇形的圆心角是_______
所对应扇形的圆心角是_______![]() ;
;
(2)把条形统计图补充完整;
(3)依次将优秀、良好、及格、不及格记为![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,则抽取的这部分学生书写成绩的众数是_______,中位数是_______,平均数是________;
分,则抽取的这部分学生书写成绩的众数是_______,中位数是_______,平均数是________;
(4)若该校共有学生![]() 人,请估计一下,书写能力等级达到优秀的学生大约有多少人?
人,请估计一下,书写能力等级达到优秀的学生大约有多少人?
【答案】(1)40,36;(2)见解析;(3)70,70,66.5;(4)280
【解析】
(1)由C等级人数及其所占百分比可得总人数,用360°乘以A等级人数所占比例即可得;
(2)总人数减去A、C、D的人数可求出B等级的人数,从而补全图形;
(3)根据众数、中位数及平均数的定义即可求得答案;
(4)利用总人数乘以样本中A等级人数所占比例即可得.
解:(1)本次抽取的学生人数是16÷40%=40(人),
扇形统计图中A所对应扇形圆心角的度数是360°×![]() =36°,
=36°,
故答案为:40、36;
(2)B等级人数为40﹣(4+16+14)=6(人),
补全的条形统计图如下:
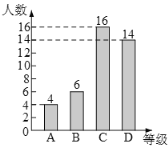
(3)∵及格的人数最多,
∴众数为70,
∵抽取的总人数共40人,
∴中位数是第20和第21个的平均数,
∴中位数为70,
平均数为![]()
故答案为:70、70、66.5;
(4)等级达到优秀的人数大约有2800×![]() =280(人).
=280(人).
答:书写能力等级达到优秀的学生大约有280人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)若![]() ,求
,求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,抛物线的对称轴为直线
两点,抛物线的对称轴为直线![]() ,且
,且![]() .
.
①求抛物线的解析式(各项系数用含![]() 的式子表示);
的式子表示);
②求线段![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日为世界阅读日,为响应党中央“倡导全民阅读,建设书香社会”的号召,某校团委组织了一次全校学生参加的“读书活动”大赛,为了了解本次大赛的成绩,校团委随机抽取了部分学生的成绩(成绩![]() 取整数,总分100分)作为样本进行统计,绘制了如下不完整的频数频率分布表和频数分布直方图:
取整数,总分100分)作为样本进行统计,绘制了如下不完整的频数频率分布表和频数分布直方图:
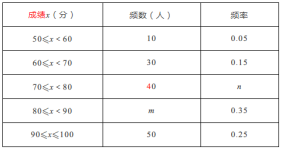
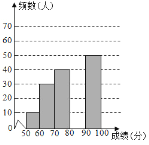
根据所给信息,解答下列问题
(1)抽取的样本容量是 .![]() .
.![]() .
.
(2)补全频数分布直方图,这200名学生成绩的中位数会落在 分数段;
(3)全校有1200名学生参加比赛,若得分为90分及以上为优秀,请你估计全校参加比赛成绩优秀的学生人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
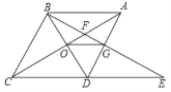
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于点
交于点 ![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() ,连接
,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点 ![]() ,
,![]() ,连接
,连接![]() ,则下列结论中一定成立的是__________.
,则下列结论中一定成立的是__________.
①![]() ;②与
;②与![]() 全等的三角形共有5个;③
全等的三角形共有5个;③![]() ;④由点
;④由点![]() 、
、![]() 、
、![]() 、
、![]() 构成的四边形是菱形
构成的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2020次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是( )

A.C、EB.E、FC.G、C、ED.E、C、F
查看答案和解析>>
科目:初中数学 来源: 题型:
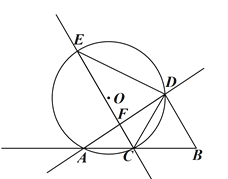
【题目】如图,AB=4,C为射线BA上一动点,以BC为边向上作正三角形BCD,⊙O过A、C、D三点,E为⊙O上一点,满足AD=ED,直线CE交直线AD于F.
(1)求证:CE∥BD;
(2)设CF=a,若C在线段AB上运动.
①求点E运动的路径长;
②求a的范围;
(3)若AC=1,求 tan∠DEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求第二次抽取卡片上的数字小于第一次抽取卡片上的数字的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com