
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=![]() x2��
x2��![]() x��
x��![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�

��1����ֱ��AE�Ľ���ʽ��
��2����PΪֱ��CE�·��������ϵ�һ�㣬����PC��PE������PCE��������ʱ����P�����ꣿ
��3����G���߶�CE���е㣬��������y=![]() x2��
x2��![]() x��
x��![]() ��x��������ƽ�Ƶõ���������y�䣬y��������D��y���Ķ���Ϊ��F������������y���ĶԳ����ϣ��Ƿ���ڵ�Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��x��������ƽ�Ƶõ���������y�䣬y��������D��y���Ķ���Ϊ��F������������y���ĶԳ����ϣ��Ƿ���ڵ�Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y= ![]() x+
x+ ![]() (2) P��2����
(2) P��2����![]() ��(3) ��3��
��(3) ��3��![]() ����3��
����3��![]() ����3��2
����3��2![]() ����3����
����3����![]() ��
��
�������������������1�������ߵĽ���ʽ�ɱ���Ϊy=![]() (x+1)(x-3)���Ӷ��ɵõ���A�͵�B�����꣬Ȼ������õ�E�����꣬��ֱ��AE�Ľ���ʽΪy=kx+b������A�͵�E������������k��b��ֵ���Ӷ��õ�AE�Ľ���ʽ��
(x+1)(x-3)���Ӷ��ɵõ���A�͵�B�����꣬Ȼ������õ�E�����꣬��ֱ��AE�Ľ���ʽΪy=kx+b������A�͵�E������������k��b��ֵ���Ӷ��õ�AE�Ľ���ʽ��
��2����ֱ��CE�Ľ���ʽΪy=mx-![]() ������E��������뼴��ȷ��ֱ��CE�Ľ���ʽ������P��PF��y�ᣬ��CE���F�����P������Ϊ��x��
������E��������뼴��ȷ��ֱ��CE�Ľ���ʽ������P��PF��y�ᣬ��CE���F�����P������Ϊ��x��![]() x2
x2![]() x
x![]() �������PF��ֵ����ʾ����EPC������������ö��κ��������ʿ����x��ֵ���Ӷ��õ���P�����ꣻ
�������PF��ֵ����ʾ����EPC������������ö��κ��������ʿ����x��ֵ���Ӷ��õ���P�����ꣻ
��3����ƽ�ƺ�������߾�����D���ɵõ���F�����꣬�����е����깫ʽ����õ�G�����꣬Ȼ���ΪFG=FQ��GF=GQ��QG=QF���������⼴��.
�⣺��1����y=![]() x2-
x2-![]() x-
x-![]() ��
��
��y=![]() (x+1)(x-3).
(x+1)(x-3).
��A��-1��0����B��3��0��.
��x=4ʱ��y=![]() .
.
��E��4��![]() ����
����
��ֱ��AE�Ľ���ʽΪy=kx+b������A�͵�E���������ã�
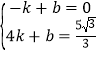 ��
��
�����k=![]() ��b=
��b=![]() ��
��
��ֱ��AE�Ľ���ʽΪy=![]() x+
x+![]()
��2����ֱ��CE�Ľ���ʽΪy=mx-![]() ������E����������4m-
������E����������4m-![]() =
=![]() �������m=
�������m=![]() .
.
��ֱ��CE�Ľ���ʽΪy=![]() x-
x-![]() .
.
����P��PF��y�ᣬ��CE���F����ͼ����ʾ.
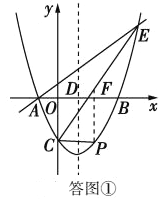
���P��������x��![]() x2
x2![]() x
x![]() �������F��x��
�������F��x��![]() x
x![]() ����
����
��FP=(![]() x
x![]() )-(
)-(![]() x2
x2![]() x
x![]() )=-
)=-![]() x2+
x2+![]() x��
x��
���EPC�����=![]() ��(-
��(-![]() x2+
x2+![]() x)��4=-
x)��4=-![]() x2+
x2+![]() x.
x.
�൱x=2ʱ����EPC��������.
��P��2��-![]() ��.
��.
��3����ͼ����ʾ��
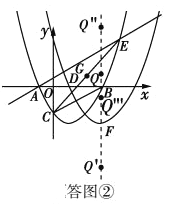
��y��������D��y���Ķ���Ϊ��F��
���F��3��-![]() ��.
��.
�ߵ�GΪCE���е㣬
��G��2��![]() ��.
��.
��FG=![]() ��.
��.
�൱FG=FQʱ����Q��3��![]() ����Q�䣨3��
����Q�䣨3��![]() ��.
��.
��GF=GQʱ����F���Q������y=![]() �Գƣ�
�Գƣ�
����Q�壨3��2![]() ��.
��.
��QG=QFʱ�����Q1�ĵ�����Ϊ��3��a��.
�������ľ��빫ʽ����֪����a+![]() =
=![]() �������a=-
�������a=-![]() .
.
���Q1��������3��-![]() ��.
��.
������������Q��������3��![]() ����3��
����3��![]() ����3��2
����3��2![]() ����3��-
����3��-![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
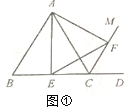
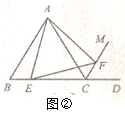
����Ŀ������֪����ͼ�٣���ABC�ǵȱ������Σ�CM����ǡ�ACD��ƽ���ߣ�E�DZ�BC�е㣬��CM�Ͻ�ȡCF=BE������AE��EF��AF.��֤����AEF�ǵȱ������Σ�����Ҫ֤����.
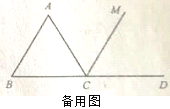
��̽������ͼ�ڣ���ABC�ǵȱ������Σ�CM����ǡ�ACD��ƽ���ߣ�E�DZ�BC��һ�㣨�����B��C�غϣ�����CM�Ͻ�ȡCF=BE������AE��EF��AF.��֤����AEF�ǵȱ�������.
��Ӧ�á���ͼ���еġ�E�DZ�BC��һ�㡱��Ϊ��E�DZ�BC�ӳ�����һ�㡱��������������.���ı���ACEF����Գ�ͼ�Σ���AB=2ʱ�����������ͼ��ֱ��д���ı���ACEF���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ӡ���ǿ���ԡ�������һ�ڡ�����ʶ�ˡ���Ŀ������ѡ���Լ�ͥΪ��λ��ÿ���ͥ�ɰְ�����ͱ���3����ɣ��ְ֡�����ͱ�����ɢ����������ѡ�����ڱ�����ѡһ��������Ȼ��ֱ��ڰְ������������������ȷ�ҳ���������ĸ�ĸ���������������أ�������ѧ�Ƕ�˼������֪�ڱ��ڱ�������A��B��C�����ͥ���б���.
��1��������������С��ѡ��A���ͥ�ı�������С����������������ȷ�ҳ�������ĸ��ʣ�
��2�������ѡһ������������ѡA���ͥ����ͨ���б�����״ͼ�ķ����������������С��������ȷ�ҶԱ�����ĸ����һ�˵ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ͱˮ,��Ͱװ��![]() ��ˮ,��Ͱ�е�ˮ�ȼ�Ͱ�е�ˮ��3��.�ֽ���Ͱ�е�һ�뵽��Ͱ��,Ȼ���ٽ���ʱ��Ͱ����ˮ����
��ˮ,��Ͱ�е�ˮ�ȼ�Ͱ�е�ˮ��3��.�ֽ���Ͱ�е�һ�뵽��Ͱ��,Ȼ���ٽ���ʱ��Ͱ����ˮ����![]() ������Ͱ,�ٶ�Ͱ�㹻��,ˮ�������.���ǽ��������������Ϊһ�β���,�����ظ�����,��( )
������Ͱ,�ٶ�Ͱ�㹻��,ˮ�������.���ǽ��������������Ϊһ�β���,�����ظ�����,��( )
A. ÿ����һ��,��Ͱ�е�ˮ�������С,����Ͱ�е�ˮ��ȫ��������Ͱ
B. ÿ����һ��,��Ͱ�е�ˮ�������С,����Զ������
C. ÿ����һ��,��Ͱ�е�ˮ����������,��������,����Ͱ�е�ˮ�����Ͱ��
D. ÿ����һ��,��Ͱ�е�ˮ����������,����Զ����Ͱ�е�ˮ��Ҫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
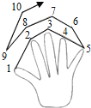
����Ŀ�� �Ӵ�Ĵָ��ʼ�����մ�Ĵָ��ʳָ����ָ������ָ��Сָ������ָ����ָ��ʳָ����Ĵָ��ʳָ������˳������������1��2��3��4��5��6��7������������4019ʱ��Ӧ����ָΪ_____������n����������ָʱ������������_____���ú�n�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD���ı���BEFG���������Σ���AB=a��DE=b��a��b����

��1��д��AG�ij��ȣ��ú���ĸa��b�Ĵ���ʽ��ʾ����
��2���۲�ͼ�Σ����ò�ͬ�ķ�����ʾͼ������Ӱ���ֵ���������ܻ����Ӧ��һ����ʽ�ֽʽ���뽫�����ʽд������
��3�����������ABCD�ı߳���������DEFG�ı߳���16cm�����ǵ�������960cm2�����������еĹ�ʽ����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ŀ������![]() ������ϵ����
������ϵ����![]() ��ӡˢ�������
��ӡˢ�������
��1��������![]() ���³�3�����㻯��3x2+6x+8���C��6x+5x2+2����
���³�3�����㻯��3x2+6x+8���C��6x+5x2+2����
��2��������˵������´��ˣ��ҿ���������𰸵Ľ���dz�������ͨ������˵��ԭ������![]() ���Ǽ���
���Ǽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
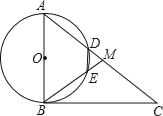
����Ŀ����ͼ����Rt��ABC�У���ABC=90������M��AC���е㣬��ABΪֱ������O�ֱ�AC��BM�ڵ�D��E������DE��ʹ�ı���DEBAΪ��O���ڽ��ı��Σ�
��1����֤����A=��ABM=��MDE��
��2����AB=6����AD=2DMʱ����DE�ij��ȣ�
��3������OD��OE������A�Ķ���Ϊ60��ʱ����֤���ı���ODME�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ѧУ��չ��Т����ĸ���Ӽ����Ͷ����𡱻��ʵʩ�������У��ȡ���꼶50��ѧ������������һ�ܣ���������㣩����������ʱ�䣨��λ��Сʱ���õ�һ�����ݣ����Ƴ��±���
ʱ��x��Сʱ�� | ���� | ���� | ��ռ�ٷֱ� |
0.5x��x��1.0 | ���� | 14 | 28% |
1.0��x��1.5 | ������ | 15 | 30% |
1.5��x��2 |
| 7 | �� �� |
2��x��2.5 |
| 4 | 8% |
2.5��x��3 | �� | 5 | 10% |
3��x��3.5 |
| 3 | �� �� |
3.5��x��4 |
| �� �� | 4% |
�ϼ� | 50 | 100% |
��1���������δ��ɵIJ��֣�
��2������������Ϣ�жϣ�ÿ���������ʱ�䲻����1.5Сʱ��ѧ����ռ�İٷֱ��Ƕ��٣�
��3��������������д��һ��20�����ڵij�����Т����ĸ���Ȱ��Ͷ����ľ��ӣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com