
【题目】已知,等腰直角△ABC在平面直角坐标系中的位置如图,点A(0,a),点B(b,0),点C在第四象限,且满足a2+b2-4a+12b+40=0.

(1)求点C的坐标;
(2)若AC交x轴于M,BC交y轴于D,E是AC上一点,且CE=AM,连DM,求证:AD+DE=BM;
(3)在y轴上取点F(0,6),点H是y轴上F下方任一点,作HG⊥BH交射线CF于G,在点H位置变化的过程中,![]() 是否为定值,若是,求其值,若不是,说明理由.
是否为定值,若是,求其值,若不是,说明理由.
【答案】(1)C(2,-4) (2)见解析 (3)是定值,值为1
【解析】
(1)根据题意可求得A、B两点坐标,作CT⊥y轴于T.只要证明△ABO≌△CAT,可得CT=OA=2,AT=OB=6,由此即可解决问题;
(2)如图2中,作CK⊥AC交y轴于K.只要证明△ABM≌△CAK,△CDE≌△CDK即可解决问题;
(3)结论:![]() =1.作AI⊥AF交FB的延长线于I,作HJ⊥BF于J,HK⊥GF于K.想办法证明△HJB≌△HKG,可得BH=GH即可解决问题;
=1.作AI⊥AF交FB的延长线于I,作HJ⊥BF于J,HK⊥GF于K.想办法证明△HJB≌△HKG,可得BH=GH即可解决问题;
(1)∵a2+b2-4a+12b+40=0.
∴![]()
∴a=2,b=-6
故A(0,2),B(-6,0)
如图1中,作CT⊥y轴于T.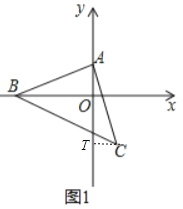
∵∠AOB=∠BAC=∠ATC=90°,
∴∠ABO+∠BAO=90°,∠BAO+∠CAT=90°,
∴∠ABO=∠CAT,
∵AB=AC,
∴△ABO≌△CAT,
∴CT=OA=2,AT=OB=6,
∴OT=AT=AO=4,
∴C(2,-4).
(2)如图2中,作CK⊥AC交y轴于K.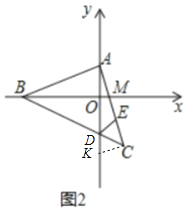
∵∠BAM=∠ACK=90°,AB=AC,∠ABM=∠CAK,
∴△ABM≌△CAK,
∴AM=CK,BM=AK,
∵CE=AM,
∴CE=CK,
∵DC=DC,∠DCE=∠DCK,
∴△CDE≌△CDK,
∴DE=DK,
∴AD+DE=AD+DK=AK=BM.
(3)是定值.结论:![]() =1.
=1.
理由:作AI⊥AF交FB的延长线于I,作HJ⊥BF交BF的延长线于J,HK⊥GF于K.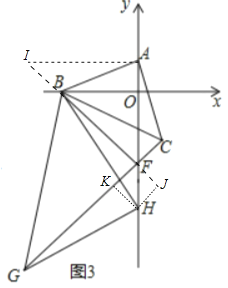
∵B(-6,0),F(0,-6),
∴OB=OF,
∴△BOF是等腰直角三角形,
∴∠AFB=45°,
∵AI⊥AF,
∴∠I=∠AFI=45°,
∴AI=AF,
∵∠BAC=∠IAF=90°,
∴∠IAB=∠FAC,
∵AI=AF,AB=AC,
∴△AIB≌△AFC,
∴∠CFA=∠I=45°
∴∠BFC=90°,
∵∠BFC=∠CFO=45°,∴∠GFH=∠HFJ=45°,
∴HK=HJ,
∵∠BFG=∠BHG,
∴∠HBF=∠HGF,
∴△HJB≌△HKG,
∴BH=GH,
∴![]() =1.
=1.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四点A、B、C、D.
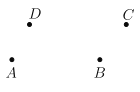
(1)用圆规和无刻度的直尺按下列要求与步骤画出图形:
①画直线AB.
②画射线DC.
③延长线段DA至点E,使![]() .(保留作图痕迹)
.(保留作图痕迹)
④画一点P,使点P既在直线AB上,又在线段CE上.
(2)在(1)中所画图形中,若![]() cm,
cm,![]() cm,点F为线段DE的中点,求AF的长.
cm,点F为线段DE的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A,B望灯塔C,测得∠NAC=30,∠NBC=60.

(1)求从海岛B到灯塔C的距离;
(2)这条船继续向正北航行,问在上午或下午的什么时间小船与灯塔C的距离最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
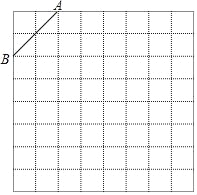
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
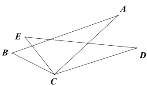
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中顶点为点M的抛物线是由抛物线![]() 向右平移1个单位得到的,它与y轴负半轴交于点A,点B在抛物线上,且横坐标为3.
向右平移1个单位得到的,它与y轴负半轴交于点A,点B在抛物线上,且横坐标为3.
![]() 写出以M为顶点的抛物线解析式.
写出以M为顶点的抛物线解析式.
![]() 连接AB,AM,BM,求
连接AB,AM,BM,求![]() ;
;
![]() 点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为
点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为![]() ,当
,当![]() 时,求点P坐标.
时,求点P坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com