
【题目】如图,直径为AB的⊙O交Rt△BCD的两条直角边BC、CD于点E、F,且 ![]() ,连接BF.
,连接BF.
(1)求证:CD为⊙O的切线;
(2)当CF=1且∠D=30°时,求AD长.
【答案】
(1)
证明:连接OF.

∵ ![]() ,
,
∴∠CBF=∠FBA,
∵OF=OB,
∴∠FBO=∠OFB,
∴∠CBF=∠OFB,
∴BC∥OF,
∴∠OFC+∠C=180°,
∵∠C=90°,
∴∠OFC=90°,即OF⊥DC,
∴CD为⊙O的切线.
(2)
解:连接AF.
∵∠D=30°,∠C=90°,
∴∠CBD=60°
∵ ![]() ,
,
∴∠CBF=∠DBF= ![]() ∠CBD=30°,
∠CBD=30°,
在Rt△BCF中,∵FC=1,∠CBF=30°,
∴BF=2CF=2.
∴BC= ![]() =
= ![]() ,
,
∵AB是⊙O的直径,
∴∠AFB=90°,
在Rt△AFB中,∵∠ABF=30°,BF=2,
∴AF= ![]() AB.
AB.
∴AB2=( ![]() AB)2+BF2,即
AB)2+BF2,即 ![]() AB2=4,AB=
AB2=4,AB= ![]() ,
,
在Rt△DCB中,∵∠D=30°,BC= ![]() ,
,
∴BD=2BC=2 ![]() .
.
∴AD=DB﹣AB=2 ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)连接OF,只要证明OF∥BC,即可推出OF⊥CD,由此即可解决问题.(2)连接AF.思想在Rt△BCF中,求出BC,再在Rt△DBC中,求出DB,在Rt△ABF中,求出AB,根据AD=DB﹣AB即可解决问题.
【考点精析】根据题目的已知条件,利用含30度角的直角三角形和圆心角、弧、弦的关系的相关知识可以得到问题的答案,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,求OQ的长度;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.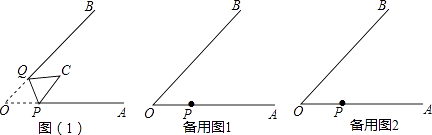
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
(1)根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图像,猜测y与x之间的函数关系,并求出该函数关系式:
x(元) | 3 | 4 | 5 | 6 |
y(个) | 20 | 15 | 12 | 10 |

(2)设经营此笔记本的日销售利润为w元,试求出w与x之间的函数关系式;
(3)当日销售单价为8元时,求日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图像中,能表示y与x的函数关系的图像大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABO中,∠ABO=90°,OB边在x轴上,将△ABO绕点B顺时针旋转60°得到△CBD.若点A的坐标为(﹣2,2 ![]() ),则点C的坐标为( )
),则点C的坐标为( )
A.( ![]() ,1)
,1)
B.(1, ![]() )
)
C.(1,2)
D.(2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的距离,记录相应的托盘B中的砝码质量,得到下表: 
托盘B与点O的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
(1)把上表中(x,y)的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑曲线连接起来;观察所画的图像,猜测y与x之间的函数关系,求出该函数解析式;
(2)当托盘B向左移动(不超过点M)时,应往托盘B中添加砝码还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA. 
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD. 
(1)求证:直线MN是⊙O的切线;
(2)若CD=4,AC=5,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com