
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,求OQ的长度;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.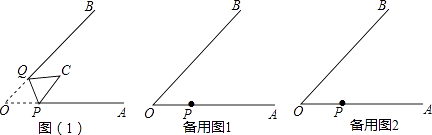
【答案】
(1)
解:①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2cm;
②当PC⊥QB时,分两种情况:
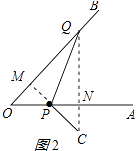
(i)如图1所示:设OQ=xcm,
∵∠O=45°,
∴△OPM是等腰直角三角形,
∴OM= ![]() OP=
OP= ![]() ,
,
∴QM= ![]() ﹣x,
﹣x,
由折叠的性质得:∠C=∠O=45°,CQ=OQ=x,
∴△CQM是等腰直角三角形,
∴QC= ![]() QM
QM
∴x= ![]() (
( ![]() ﹣x),
﹣x),
解得:x=2 ![]() ﹣2,
﹣2,
即OQ=2 ![]() ﹣2;
﹣2;
(ii)如图2所示:同(i)得:OQ=2 ![]() +2;
+2;
综上所述:当PC⊥QB时,OQ的长为2 ![]() ﹣2,或2
﹣2,或2 ![]() +2.
+2.
(2)
解:当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在∠AOB的内部时,四边形OPCQ是菱形,OQ=OP=2cm;
②当点C在∠AOB的一边上时,△OPQ是等腰直角三角形,OQ= ![]() 或2
或2 ![]() ;
;
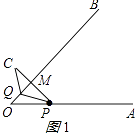
③当点C在∠AOB的外部时,分两种情况:
(i)如图3所示:PM=PQ,则∠PMQ=∠PQM=∠O+∠OPQ,
由折叠的性质得:∠OPQ=∠MPQ,
设∠OPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△OPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠OPQ=30°,
作QN⊥OP于N,设ON=a,
∵∠O=45°,
则QN=ON=a,OQ= ![]() a,PN=
a,PN= ![]() QN=
QN= ![]() a,
a,
∵ON+PN=OP,
∴a+ ![]() a=2,
a=2,
解得:a= ![]() ﹣1,
﹣1,
∴OQ= ![]() (
( ![]() ﹣1)=
﹣1)= ![]() ﹣
﹣ ![]() ;
;
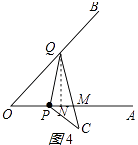
(ii)如图4所示:PQ=MQ,作QN⊥OA于N,
同①得:OQ= ![]() +
+ ![]() ;
;
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或(2 ![]() ﹣2,)cm或(2
﹣2,)cm或(2 ![]() +2)cm或(
+2)cm或( ![]() ﹣
﹣ ![]() )cm或(
)cm或( ![]() +
+ ![]() )cm.
)cm.

【解析】(1)①由平行线的性质得出∠O=∠CPA,由折叠的性质得出∠C=∠O,OP=CP,证出∠CPA=∠C,得出OP∥QC,证出四边形OPCQ是菱形,得出OQ=OP=2cm即可;
②当PC⊥QB时,分两种情况:设OQ=xcm,证出△OPM是等腰直角三角形,得出OM= ![]() OP=
OP= ![]() ,QM=
,QM= ![]() ﹣x,证出△CQM是等腰直角三角形,得出QC=
﹣x,证出△CQM是等腰直角三角形,得出QC= ![]() QM,得出方程x=
QM,得出方程x= ![]() (
( ![]() ﹣x),解方程即可;(ii)同(i)得出:OQ=2
﹣x),解方程即可;(ii)同(i)得出:OQ=2 ![]() +2;即可得出结论;(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可.
+2;即可得出结论;(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连接BD,如果∠DAC=∠DBA,那么 ![]() 的值是 .
的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. 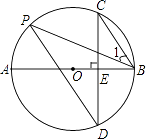
(1)求证:CB∥PD;
(2)若BC=6,sin∠P= ![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( ) 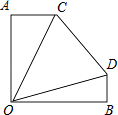
A.90km
B.50 ![]() km
km
C.20 ![]() km
km
D.100km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF. 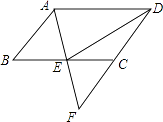
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+2
x+2 ![]() 与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和
与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和 ![]() 个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为AB的⊙O交Rt△BCD的两条直角边BC、CD于点E、F,且 ![]() ,连接BF.
,连接BF.
(1)求证:CD为⊙O的切线;
(2)当CF=1且∠D=30°时,求AD长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com