
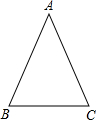
 如图,在△ABC中,∠B=∠C=67.5°.
如图,在△ABC中,∠B=∠C=67.5°.分析 (1)要求sinA的值,根据三角形内角和可求得∠A的度数,从而可以求得sinA的值;
(2)要求tanC的值,只要作辅助线BD⊥AC于点D,然后通过变形,即可求得tanC的值.
解答 解:(1)∵在△ABC中,∠B=∠C=67.5°,
∴∠A=180°-∠B-∠C=180°-67.5°-67.5°=45°,
∴sinA=sin45°=$\frac{\sqrt{2}}{2}$,
即sinA=$\frac{\sqrt{2}}{2}$;
(2)作BD⊥AC于点D,如下图所示,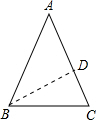
∵由(1)可知∠A=45°,设BD=a,
∴AD=a,AB=$\sqrt{2}a$,
∵AB=AC,
∴AC=$\sqrt{2}a$,
∴CD=AC-AD=$\sqrt{2}a-a$,
∴$tanC=\frac{BD}{CD}=\frac{a}{\sqrt{2}a-a}=\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+1$,
即tanC=$\sqrt{2}+1$.
点评 本题考查解直角三角形、三角形的内角和、求角的三角函数值,解题的关键是明确题意,找出对应量,求出相应的三角函数值.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a=1,m=-2 | B. | a=1,m=2 | C. | a=-1,m=-2 | D. | a=-1,m=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2对 | B. | 4对 | C. | 6对 | D. | 8对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边相等的四边形是正方形 | |
| B. | 四角相等的四边形是正方形 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 有一个角是直角的菱形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF.
如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com