
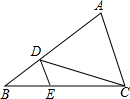
 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=| S△DEC |
| S△ADC |
| ||
|
| DE |
| AC |
| DE |
| AC |
| 1 |
| 3 |
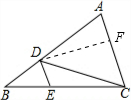 解:过点D作DF⊥AC于点F;
解:过点D作DF⊥AC于点F;| S△DEC |
| S△ADC |
| ||
|
| DE |
| AC |
| S△BDE |
| S△ABC |
| DE |
| AC |
| 1 |
| 9 |


科目:初中数学 来源: 题型:
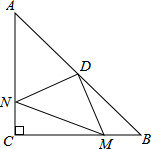 在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.
在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
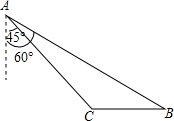 如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:
如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
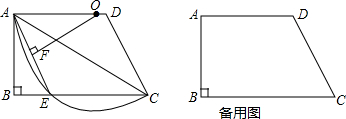
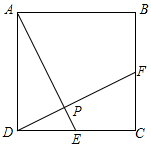 正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.
正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
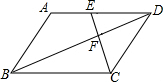 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com