
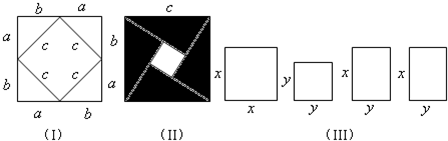
���� ��1����Ӱ��������ɴ������������ȥС�����������Ҳ�������ĸ�ֱ�����������֮�������������ȼ��ɵ�֤��
��2��ƴ����ͼ��ʾͼ�Σ����ݴ������α߳�Ϊx+2y����ʾ���������������������С�������������������֮�������������֤��
��� �⣺��1��S��Ӱ=4��$\frac{1}{2}$ab��S��Ӱ=c2-��a-b��2��
��4��$\frac{1}{2}$ab=c2-��a-b��2����2ab=c2-a2+2ab-b2��
��a2+b2=c2��
��2����ͼ��ʾ��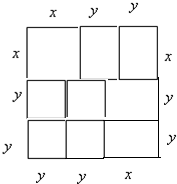
�������ε����Ϊx2+4y2+4xy��Ҳ����Ϊ��x+2y��2��
��x+2y��2=x2+4xy+4y2��
���� ���⿼������ʽ�Ļ�����㣬�����������㷨���ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2��x��3 | C�� | x��2 | D�� | x��2��x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
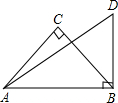 ��֪����ͼ����ABD=��C=90�㣬AD=12��BD=6��AC=BC��
��֪����ͼ����ABD=��C=90�㣬AD=12��BD=6��AC=BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 0 �� 1 | D�� | 0�͡�1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
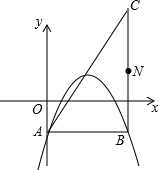 ��ͼ����ƽ��ֱ������ϵ�У���֪y=-$\frac{1}{2}$x2+bx+c��b��cΪ�������Ķ���ΪP���� ��ֱ��������ABC�Ķ���A������Ϊ��0��-1������C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
��ͼ����ƽ��ֱ������ϵ�У���֪y=-$\frac{1}{2}$x2+bx+c��b��cΪ�������Ķ���ΪP���� ��ֱ��������ABC�Ķ���A������Ϊ��0��-1������C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com