
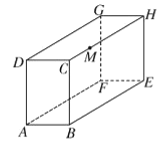
【题目】已知如图,长方体的长![]() ,宽
,宽![]() ,高
,高![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,一只蚂蚁如果沿沿着长方体的表面从点
,一只蚂蚁如果沿沿着长方体的表面从点![]() 爬到点
爬到点![]() ,需要爬行的最短距离是多少?
,需要爬行的最短距离是多少?
【答案】需要爬行的最短距离是![]() cm.
cm.
【解析】
将长方体沿CH、HE、BE剪开,然后翻折,使面ABCD和面BEHC在同一个平面内,连接AM;或将长方体沿CH、GD、GH剪开,然后翻折,使面ABCD和面DCHG在同一个平面内,连接AM;或将长方体沿AB、AF、EF剪开,然后翻折,使面ABEF和面BEHC在同一个平面内,连接AM;再分别在Rt△ADM、Rt△ABM、Rt△ACM中,利用勾股定理求得AM的长,比较大小即可求得需要爬行的最短路程.
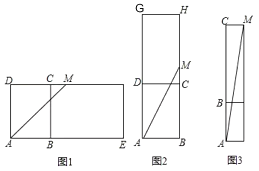
解:将长方体沿CH、HE、BE剪开,然后翻折,使面ABCD和面BEHC在同一个平面内,连接AM,如图1,
由题意可得:MD=MC+CD=5+10=15cm,AD=15cm,
在Rt△ADM中,根据勾股定理得:AM=![]() cm;
cm;
将长方体沿CH、GD、GH剪开,然后翻折,使面ABCD和面DCHG在同一个平面内,连接AM,如图2,
由题意得:BM=BC+MC=5+15=20cm,AB=10cm,
在Rt△ABM中,根据勾股定理得:AM=![]() cm,
cm,
将长方体沿AB、AF、EF剪开,然后翻折,使面ABEF和面BEHC在同一个平面内,连接AM,如图3,
由题意得:AC=AB+CB=10+15=25cm,MC=5cm,
在Rt△ACM中,根据勾股定理得:AM=![]() cm,
cm,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
则需要爬行的最短距离是![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:①b2=4ac,②abc<0;③a>c;④4a﹣2b+c<0,其中正确的个数有( )
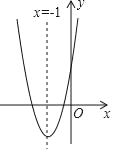
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种苗木,由信息解答以下问题:
苗 木 品 种 | A | B | C |
每辆汽车运载量(吨) | 12 | 10 | 8 |
每吨苗木获利(万元) | 3 | 4 | 2 |
(1)设装A种苗木车辆数为x,装运B种苗木的车辆数为y,求y与x之间的函数关系式;
(2)若装运每种苗木的车辆都不少于2辆,则车辆安排方案有几种?写出每种安排方案
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
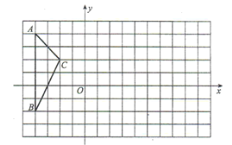
【题目】如图,△ABC中,A(-4,4),B(-4,-2),C(-2,2).
(1)请画出将△ABC向右平移8个单位长度后的△A1BlC1;
(2)以O为位似中心,将△A1BlC1缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2.
,得到△A2B2C2,请在y轴右侧画出△A2B2C2.
(3)画出一个三角形,使它与△ABC相似,且相似比是无理数,并写出所画三角形与△ABC的相似比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
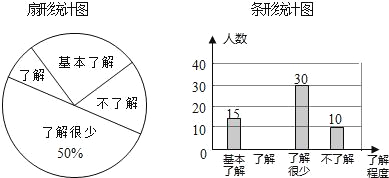
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com