
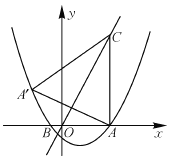
【题目】抛物线y=![]() x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() .(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到
.(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到![]() 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.
【解析】试题分析:(1)将点A、B的坐标代入抛物线的解析式,得到关于b、c的二元一次方程组,从而可解得b、c的值;
(2)过点B′作B′E⊥x轴于E,BB′与OC交于点F.由平行于y轴的直线上各点横坐标相同可知点C的横坐标为2,将x=2代入直线y=﹣2x的解析式可求得点C的坐标∵点B和B′关于直线y=﹣2x对称,在Rt△ABC中,由勾股定理可求得OC=5![]() ,然后利用面积法可求得BF=2
,然后利用面积法可求得BF=2![]() .由轴对称图形的性质可知B′F=FB=4
.由轴对称图形的性质可知B′F=FB=4![]() .由同角的余角相等可证明∠B′BE=∠BCF,从而可证明Rt△B′EB∽Rt△OBC,由相似三角形的性质可求得B′E=4,BE=8,故此可求得点B′的坐标为(﹣3,﹣4),然后可判断出点B′在抛物线上;
.由同角的余角相等可证明∠B′BE=∠BCF,从而可证明Rt△B′EB∽Rt△OBC,由相似三角形的性质可求得B′E=4,BE=8,故此可求得点B′的坐标为(﹣3,﹣4),然后可判断出点B′在抛物线上;
(3)先根据题意画出图形,然后利用待定系数法求得B′C的解析式,设点P的坐标为(x,﹣![]() +x+
+x+![]() ),则点D为(x,﹣
),则点D为(x,﹣![]() ),由平行四边形的判定定理可知当PD=BC时.四边形PBCD是平行四边形,最后根据PD=BC列出关于x的方程即可求得点P的坐标
),由平行四边形的判定定理可知当PD=BC时.四边形PBCD是平行四边形,最后根据PD=BC列出关于x的方程即可求得点P的坐标
解:(1)∵y=![]() x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,
x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,
∴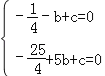 .
.
解得:![]() .
.
∴抛物线的解析式为y=﹣![]() +x+
+x+![]() .
.
(2)如图,过点B′作B′E⊥x轴于E,BB′与OC交于点F.
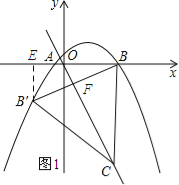
∵BC⊥x轴,
∴点C的横坐标为5.
∵点C在直线y=﹣2x上,
∴C(5,﹣10).
∵点B和B′关于直线y=﹣2x对称,
∴B′F=BF.
在Rt△ABC中,由勾股定理可知:OC=![]() =
=![]() =5
=5![]() .
.
∵S△OBC=![]() OCBF=
OCBF=![]() OBBC,
OBBC,
∴5![]() ×BF=5×10.
×BF=5×10.
∴BF=2![]() .
.
∴BB′=4![]() .
.
∵∠B′BE+∠B′BC=90°,∠BCF+∠B′BC=90°,
∴∠B′BE=∠BCF.
又∵∠B′EB=∠OBC=90°,
∴Rt△B′EB∽Rt△OBC.
∴![]() ,即
,即![]() .
.
∴B′E=4,BE=8.
∴OE=BE﹣OB=3.
∴点B′的坐标为(﹣3,﹣4).
当x=﹣3时,y=﹣![]() ×(﹣3)2+
×(﹣3)2+![]() =﹣4.
=﹣4.
所以,点B′在该抛物线上.
(3)存在.
理由:如图所示:
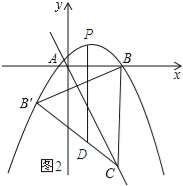
设直线B′C的解析式为y=kx+b,则![]() ,解得:
,解得: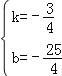
∴直线B′C的解析式为y=![]() .
.
设点P的坐标为(x,﹣![]() +x+
+x+![]() ),则点D为(x,﹣
),则点D为(x,﹣![]() ).
).
∵PD∥BC,
∴要使四边形PBCD是平行四边形,只需PD=BC.又点D在点P的下方,
∴![]() ﹣(﹣
﹣(﹣![]() )=10..
)=10..
解得x1=2,x2=5(不合题意,舍去).
当x=2时,![]() =
=![]() .
.
∴当点P运动到(2,![]() )时,四边形PBCD是平行四边形.
)时,四边形PBCD是平行四边形.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,2016年某县投入教育经费6000万元,2018年投入教育经费8640万元,假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2019年该县投入教育经费多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上对应点如图所示,且|a|>|b|.
![]()
(1)|a﹣b|= ,|a+b|= ,|a+c|= ,|b﹣c|= ;
(2)化简|a﹣b|﹣|a+b|+|a+c|﹣|b﹣c|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
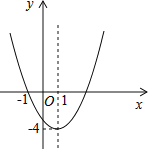
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正五棱柱的底面边长为2cm,高为4cm。

(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有![]() 的代数式表示
的代数式表示![]() 棱柱的顶点数、面数、与棱的条数。
棱柱的顶点数、面数、与棱的条数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,则下列结论中错误的是( )
![]()
A. a+c<0B. -a+b+c<0
C. |a+b|>|a+c|D. |a+b|<|a+c|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,将点
中,将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .将点
.将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 为平行四边形;
为平行四边形;
![]() 若四边形
若四边形![]() 为菱形,且
为菱形,且![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com