
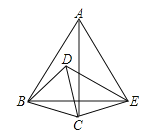
【题目】如图,在![]() 中,
中,![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转60°得到线段
逆时针旋转60°得到线段![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,若
,若![]()
![]() ,则
,则![]() 的度数为_____.
的度数为_____.
【答案】60°
【解析】
连接AD,由旋转的性质可得BC=BD,∠DBC=60°,可证△BCD为等边三角形,由“SSS”可证△ABD≌△ACD,可得∠ABD=∠ACD,由角的数量关系和等腰三角形的性质可求∠ABD=∠ACD=∠CBE=15°,由三角形内角和可求解.
连接AD,AC与BE交于F点
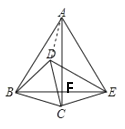
∵线段BC绕B逆时针旋转60°得到线段BD,
则BC=BD,∠DBC=60°,
∴△BCD为等边三角形,
∴BD=CD,∠DCB=∠DBC=60°,
在△ABD与△ACD中
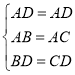 ,
,
∴△ABD≌△ACD(SSS),
∴∠ABD=∠ACD,
∵∠BCE=150°,
∴∠DCE=90°,
∵∠DEC=45°,
∴∠CDE=∠DEC=45°,
∴CD=CE=CB,且∠BCE=150°,
∴∠CBE=∠CEB=15°,
∵∠ABE=∠DBC=60°
∴∠ABD=∠ACD=∠CBE=15°,
∴∠ABC=∠ACB=75°,
∴∠BAC=180°∠ABC∠ACB=30°,
∴∠AFB=180°-∠ABE-∠BAC=90°,
∵BC=CE,
∴AC垂直平分BE,
∴AB=AE
∴△ABE是等边三角形,
∴![]() =60°
=60°
故答案为:60°.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(1,﹣4)和(﹣1,0).
(1)求这个二次函数的表达式;
(2)x在什么范围内,y随x增大而减小?该函数有最大值还是有最小值?求出这个最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市绿化工程进行招标,现有甲、乙两个工程队投标,已知甲队单独完成这项工程需要60天.经测算:如果甲队先做20天,再由甲队、乙队合作12天,那么此时共完成总工作量的![]() .
.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款4.5万元,乙队施工一天需付工程款2万元,该工程由甲乙两队合作若干天后,再由乙队完成剩余的工作,若要求完成此项工程的工程款不超过186万元,求甲、乙两队最多合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
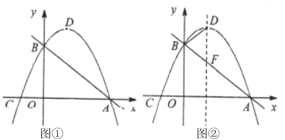
【题目】如图①,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]()
![]() 过
过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,求出点
,求出点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(3)如图②,直线![]() 与抛物线的对称轴相交于点
与抛物线的对称轴相交于点![]() ,请直接写出
,请直接写出![]() 的平分线与
的平分线与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
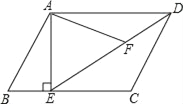
【题目】如图,平行四边形ABCD,AE⊥BC交点E,连接DE,F为DE上一点,且∠AFE=∠B=60°.
(1)求证:△ADF∽△DEC;
(2)若AE=3,AD=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八、九年级共有1000名学生.学校统计了各年级学生的人数,绘制了图①、图②两幅不完整的统计图.
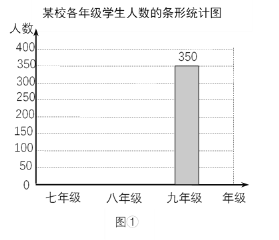
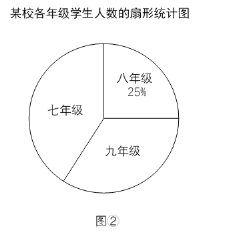
(1)将图①的条形统计图补充完整.
(2)图②中,表示七年级学生人数的扇形的圆心角度数为 °.
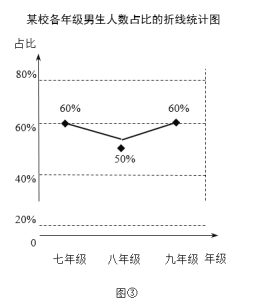
(3)学校数学兴趣小组调查了各年级男生的人数,绘制了如图③所示的各年级男生人数占比的折线统计图(年级男生人数占比=该年级男生人数÷该年级总人数×100%).请结合相关信息,绘制一幅适当的统计图,表示各年级男生及女生的人数,并在图中标明相应的数据.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com