
 如图,点A(0,a),B(b,0)分别在y轴正半轴、x轴正半轴上,C为AB的中点,a,b满足a2-2ab+b2=-|b-4|.
如图,点A(0,a),B(b,0)分别在y轴正半轴、x轴正半轴上,C为AB的中点,a,b满足a2-2ab+b2=-|b-4|.分析 (1)把a2-2ab+b2=-|b-4|化为(a-b)2+|b-4|=0,得到a=b=4,从而得出A,B两点坐标,也得到OA=OB=4,即可证得结论;
(2)作MC⊥y轴于M,作NC⊥x轴于N,C为AB的中点,可得MC=CN,在证得△MCE≌△NCF,于是证出ME=NF,于是有OE+OF=OM-ME+ON+NF=OM+ON=2+2=4.
解答 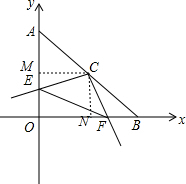 解:(1)∵a2-2ab+b2=-|b-4|,
解:(1)∵a2-2ab+b2=-|b-4|,
∴(a-b)2+|b-4|=0,
∴a=b=4,
∴A,B两点坐标A(0,4),B(4,),
∴OA=OB=4,
∵AO⊥BO,
∴△AOB是等腰直角三角形;
(2)作MC⊥y轴于M,作NC⊥x轴于N,如图所示:
∵C为AB的中点,
则MC=CN=$\frac{1}{2}BC$=2,四边形OMCN是正方形,∠EMC=∠CNF=90°,
∴OM=ON=MC=CN=2,∠MCN=90°,
∵∠ECF=90°,
∴∠MCE=∠FCN,
在△MCE和△NCF中,
$\left\{\begin{array}{l}{∠MCE=∠FCN}\\{∠CME=∠CNF}\\{CM=CN}\end{array}\right.$,
∴△MCE≌△NCF,
∴ME=NF,
∴OE+OF=OM-ME+ON+NF=OM+ON=2+2=4.
点评 本题考查了非负数的性质,等腰三角形的判定,坐标与图形性质,全等三角形的判定与性质,正方形的判定与性质;通过作辅助线得出正方形和三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2(n+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )| A. | 不能 | B. | 带① | C. | 带② | D. | 带③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com