
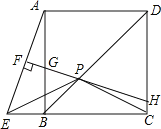
【题目】如图,正方形ABCD中,P在对角线BD上,E在CB的延长线上,且PE=PC,过点P作PF⊥AE于F,直线PF分别交AB、CD于G、H,
(1)求证:DH=AG+BE;
(2)若BE=1,AB=3,求PE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题
(1)如图,在DC上截取DM=BE,连接AM,则由已知可证△ABE≌ADM,再证四边形AGHM是平行四边形就可得MH=AG,再由DH=MH+DM=AG+BE即可得到结论;
(2)如图,连接AP,由已知可证:△ABP≌△CBP,得到PA=PC,∠3=∠4,结合PC=PE可证得PA=PE,∠3=∠5;再由∠5+∠BNE=∠3+∠ANP=90°,可证∠APE=90°,由此可得△APE是等腰直角三角形;在△ABE中由勾股定理求得AE的长就可解得PE的长.
试题解析:
(1)在DC上截取DM=BE,连接AM,
∵四边形ABCD是正方形,
∴∠ABE=∠ADM=90°,AB=AD,
∵在△ABE和△ADM中: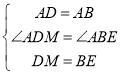 ,
,
∴△ABE≌ADM,
∴∠1=∠2,
∴∠1+∠BAM=∠2+∠BAM=90°,
∴AM⊥AE.
又∵PF⊥AE于F,
∴AM∥FH,
又∵AB∥CD,
∴四边形AGHM是平行四边形,
∴ AG=MH,
∵ DH=DM+MH,
∴ DH=AG+BE.
(2)连接AP.
∵四边形ABCD是正方形,
∴AB=BC,∠ABP=∠CBP=45°,
∵在△ABP和△CBP中: ,
,
∴△ABP≌△CBP,
∴PA=PC,∠3=∠4,
∵PE=PC,
∴PA=PE,∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴∠3+∠ANP=∠5+∠ENB=90°,
∴AP⊥PE,即△APE是等腰直角三角形,
∵BE=1,AB=3,
∴ AE=![]() ,
,
∴ PE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1.若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
材料2.已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2-x-1=0的两个不相等的实数根,
根据材料1得m+n=1,mn=-1,
∴![]() .
.
解决问题:
(1)一元二次方程x2-4x-3=0的两根为x1,x2,则x1+x2= ,x1x2= .
(2)已知实数m,n满足2m2-2m-1=0,2n2-2n-1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )

A.(![]() )2014 B.(
)2014 B.(![]() )2015 C.(
)2015 C.(![]() )2015 D.(
)2015 D.(![]() )2014
)2014
查看答案和解析>>
科目:初中数学 来源: 题型:
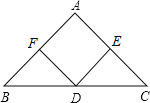
【题目】如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.
(1)求证:DE=DF;
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,⊙O过点B,C,且与BA,CA的延长线分别交于点D,E,弦DF∥AC,EF的延长线交BC的延长线于点G.
(1)求证:△BEF是等边三角形;
(2)若BA=4,CG=2,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 | 90<x≤100 | 8 |
第2组 | 80<x≤90 | a |
第3组 | 70<x≤80 | 10 |
第4组 | 60<x≤70 | b |
第5组 | 50<x≤60 | 3 |
请根据以上信息,解答下列问题:

(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com