
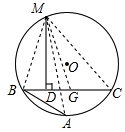
 请阅读下列材料,并完成相应的任务:
请阅读下列材料,并完成相应的任务:分析 首先证明△MBA≌△MGC(SAS),进而得出MB=MG,再利用等腰三角形的性质得出BD=GD,即可得出答案.
解答 解:如图,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是$\widehat{ABC}$的中点,
∴MA=MC.
在△MBA和△MGC中$\left\{\begin{array}{l}{BA=GC}\\{∠A=∠C}\\{MA=MC}\end{array}\right.$,
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD.
点评 此题主要考查了全等三角形的判定与性质以及等腰三角形以及等边三角形的性质,正确作出辅助线利用全等三角形的判定与性质解题是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
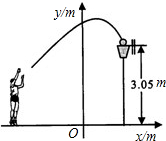 一位篮球运动员投篮,球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行,然后准确落入篮筐内,已知篮筐的中心距离底面的距离为3.05m.
一位篮球运动员投篮,球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行,然后准确落入篮筐内,已知篮筐的中心距离底面的距离为3.05m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-4(x-2)2-5 | B. | y=-4(x+2)2-5 | C. | y=-4(x-5)2+2 | D. | y=-4(x+5)2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
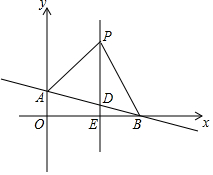 如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).
如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
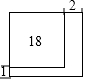 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长为6m(精确到1m)
公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长为6m(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com