【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”．为此，某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生．根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：
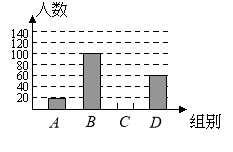
Ａ组：
；Ｂ组：
Ｃ组：
Ｄ组：
请根据上述信息解答下列问题：
（1）Ｃ组的人数是；
（2）本次调查数据的中位数落在组内；
（3）若该辖区约有24 000名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？
科目：初中数学 来源： 题型：
【题目】对非负实数x“四舍五入”到个位的值记为[x]．即当n为非负整数时，若n﹣
≤x＜n+，则[x]＝n．如：[2.9]＝3；[2.4]＝2；……根据以上材料，解决下列问题：
（1）填空[1.8]＝ ，[
]＝ ；
（2）若[2x+1]＝4，则x的取值范围是 ；
（3）求满足[x]＝
x﹣1的所有非负实数x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“校园安全”受到全社会的广泛关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：
(1)接受问卷调查的学生共有_______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°；
(2)请补全条形统计图；
(3)若该中学共有学生1800人，请根据上述调查结果，估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数；
查看答案和解析>>
科目：初中数学 来源： 题型：
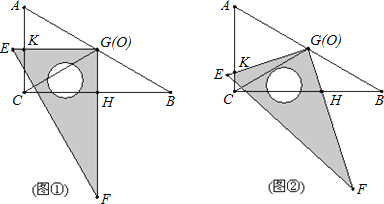
【题目】把两个全等的直角三角板ABC和EFG叠放在一起，使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，其中∠B＝∠F＝30°，斜边AB和EF长均为4.
(1)当 EG⊥AC于点K，GF⊥BC于点H时（如图①），求GH：GK的值.
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转，旋转角α满足条件：0°＜α<30°（如图②），EG交AC于点K ，GF交BC于点H，GH：GK的值是否改变？证明你发现的结论；
（3）三角板EFG由图①所示的位置绕O点逆时针旋转一周，是否存在某位置使△BFG是等腰三角形，若存在，请直接写出相应的旋转角α(精确到0.1°)；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角坐标系中，A是反比例函数y＝
（x＞0）图象上一点，B是y轴正半轴上一点，以OA，AB为邻边作ABCO．若点C及BC中点D都在反比例函数y＝
（k＜0，x＜0）图象上，则k的值为（ ）
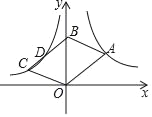
A. ﹣3B. ﹣4C. ﹣6D. ﹣8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售，其中甲种礼品盒每盒装4罐，每盒售价240元；乙种礼品盒每盒装6罐，每盒售价300元，恰好全部装完.已知每罐茶叶的成本价为30元，设甲种礼品盒的数量为x盒，乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元，则甲种礼品盒的数量至少要多少盒？
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元，且甲、乙两种礼品盒的数量和不超过69盒，求m的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，O为坐标原点，B在x轴上，四边形OACB为平行四边形，且
∠AOB=60°，反比例函数
（k＞0）在第一象限内过点A，且与BC交于点F。当F为BC的中点，且S△AOF＝12
时，OA的长为____.
查看答案和解析>>
科目：初中数学 来源： 题型：
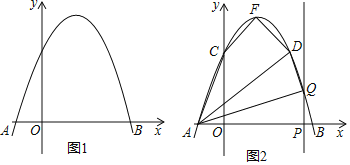
【题目】如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．
（1）求该抛物线所对应的函数解析式；
（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．
①求四边形ACFD的面积；
②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
