Question

如图，经过点C（0，﹣4）的抛物线y=ax²+bx+c（a≠0）与x轴相交于A（﹣2，0），B两点．

（1）a　　　　　　0，b²﹣4ac　　　　　　0（填“＞”或“＜”）；

（2）若该抛物线关于直线x=2对称，求抛物线的函数表达式；

（3）在（2）的条件下，连接AC，E是抛物线上一动点，过点E作AC的平行线交x轴于点F．是否存在这样的点E，使得以A，C，E，F为顶点所组成的四边形是平行四边形？若存在，求出满足条件的点E的坐标；若不存在，请说明理由．

　

 

Answer 1

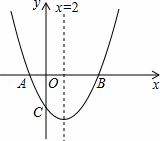
       解：（1）a＞0，b²﹣4ac＞0；

（2）∵直线x=2是对称轴，A（﹣2，0），

∴B（6，0），

∵点C（0，﹣4），将A，B，C的坐标分别代入y=ax²+bx+c，

解得：a=，b=﹣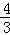，c=﹣4，

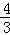∴抛物线的函数表达式为y=x²﹣x﹣4；

（3）存在，理由为：

（i）假设存在点E使得以A，C，E，F为顶点所组成的四边形是平行四边形，

过点C作CE∥x轴，交抛物线于点E，过点E作EF∥AC，交x轴于点F，如图1所示，

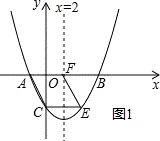
则四边形ACEF即为满足条件的平行四边形，

∵抛物线y=x²﹣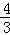x﹣4关于直线x=2对称，

∴由抛物线的对称性可知，E点的横坐标为4，

又∵OC=4，

∴E的纵坐标为﹣4，

∴存在点E（4，﹣4）；

（ii）假设在抛物线上还存在点E′，使得以A，C，F′，E′为顶点所组成的四边形是

平行四边形，过点E′作E′F′∥AC交x轴于点F′，

则四边形ACF′E′即为满足条件的平行四边形，

∴AC=E′F′，AC∥E′F′，如图2，过点E′作E′G⊥x轴于点G，

∵AC∥E′F′，∴∠CAO=∠E′F′G，

又∵∠COA=∠E′GF′=90°，AC=E′F′，∴△CAO≌△E′F′G，

∴E′G=CO=4，∴点E′的纵坐标是4，

∴4=x²﹣x﹣4，

解得：x₁=2+2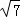，x₂=2﹣2，

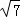∴点E′的坐标为（2+2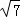，4），同理可得点E″的坐标为（2﹣2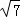，4）．