
【题目】某校九年级数学测试后,为了解学生学习情况,随机抽取了九年级部分学生的数学成绩进行统计,得到相关的统计图表如下.
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题:
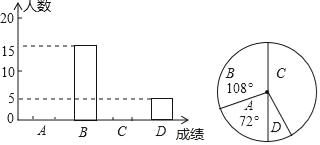
(1)这次统计共抽取了 名学生的数学成绩,补全频数分布直方图;
(2)若该校九年级有1000名学生,请据此估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有多少人?
(3)根据学习中存在的问题,通过一段时间的针对性复习与训练,若A等级学生数可提高40%,B等级学生数可提高10%,请估计经过训练后九年级数学成绩在B等级以上(含B等级)的学生可达多少人?
【答案】(1)50人;补图见解析;(2)500人;(3)610名.
【解析】
(1)用总人数乘以A所占的百分比,即可得到总人数;再用总人数乘以A等级人数所占比例可得其人数,继而根据各等级人数之和等于总人数可得D等级人数,据此可补全条形图;
(2)用总人数乘以(A的百分比+B的百分比),即可解答;
(3)先计算出提高后A,B所占的百分比,再乘以总人数,即可解答.
(1)本次调查抽取的总人数为15÷![]() =50(人),
=50(人),
则A等级人数为50×![]() =10(人),D等级人数为50﹣(10+15+5)=20(人),
=10(人),D等级人数为50﹣(10+15+5)=20(人),
补全直方图如下:

故答案为:50.
(2)估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有1000×![]() =500(人);
=500(人);
(3)∵A级学生数可提高40%,B级学生数可提高10%,
∴B级学生所占的百分比为:30%×(1+10%)=33%,A级学生所占的百分比为:20%×(1+40%)=28%,
∴1000×(33%+28%)=610(人),
∴估计经过训练后九年级数学成绩在B以上(含B级)的学生可达610名.


科目:初中数学 来源: 题型:
【题目】2019年8月.山西龙城将迎来全国第二届青年运动会,盛会将至,整个城市已经进入了全力准备的状态.太职学院足球场作为一个重要比赛场馆.占地面积约24300平方米.总建筑面积4790平方米,设有2476个座位,整体建筑简洁大方,独具特色.2018年3月15日该场馆如期开工,某施工队负责安装该场馆所有座位,在安装完476个座位后,采用新技术,效率比原来提升了![]() .结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.
.结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”“10元”“20元”“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出2个小球(第一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD平分∠BAC交BC于点D,在AB上取一点E,使得EA=ED.
(1)求证:DE∥AC;
(2)若ED=EB,BD=2,EA=3,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
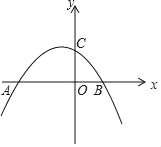
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
(1)求抛物线的函数解析式并直接写出顶点M坐标;
(2)连接AM,N是AM的中点,连接BN,求线段BN长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
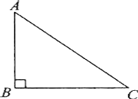
【题目】如图,△ABC中,∠B=90°,AB=3,BC=4,AC=5;
实践与操作:过点A作一条直线,使这条直线将△ABC分成面积相等的两部分,直线与BC交于点D.(尺规作图,不写作法,保留作图痕迹,标清字母)
推理与计算:求点D到AC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(-2,-2),则k的值为 。
的图象上.若点A的坐标为(-2,-2),则k的值为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D、E分别是BC、AC上的动点且BD=CE,连接AD与BE相交于点F,连接CF,下列结论:①△ABD≌△BCE;②∠AFB=120°;③若BD=CD,则FA=FB=FC;④∠AFC=90°,则AF=3BF,其中正确的结论共有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com