
����Ŀ����ƽ��ֱ������ϵxOy�У�A��m��0����B��m+4��0���������߶�AB��x���Ϸ��ĵ�P�������¶��壺��![]() ʱ���Ƶ�PΪ�߶�AB�ġ����µ㡱��
ʱ���Ƶ�PΪ�߶�AB�ġ����µ㡱��
��1����![]() ʱ��
ʱ��
���ڵ�C��3��1����D��5��3����E��2��4���У��߶�AB�ġ����µ㡱�� ��
����ֱ��![]() �ϴ����߶�AB�ġ����µ㡱����b��ȡֵ��Χ��
�ϴ����߶�AB�ġ����µ㡱����b��ȡֵ��Χ��
��2���������������������ѡһ������
��ܰ��ʾ����������ظ��Ʒ֣�
����һ��ֱ��![]() ��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�AB�����С����µ㡱����
��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�AB�����С����µ㡱����![]() �ڲ���ֱ��д��m��ȡֵ��Χ��
�ڲ���ֱ��д��m��ȡֵ��Χ��
���������G��3����1������PΪ�߶�AB�ġ����µ㡱��ֱ��GP���߶�AB�ֳ�1��3�����֣���![]() ʱ��ֱ��д����P�ĺ������ȡֵ��Χ��
ʱ��ֱ��д����P�ĺ������ȡֵ��Χ��
���𰸡���1����D��E����![]() ����2������1��
����2������1��![]() ����2������2����P�ĺ������ȡֵ��ΧΪ
����2������2����P�ĺ������ȡֵ��ΧΪ![]() ��
��![]() ��
��
��������
��1������ͼ�����������͡���ͼ�μ����жϣ�
����ֱ��![]() ������B��6��0��ʱ��
������B��6��0��ʱ��![]() ����ֱ����
����ֱ����![]() ����ʱ����
����ʱ����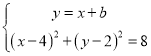 ����ȥy�����õ�
����ȥy�����õ�![]() ��������
��������![]() ���ɵ�
���ɵ�![]() �����
�����![]() ��6���ɴ˼����жϣ�
��6���ɴ˼����жϣ�
��2������һ����֪�������͡��Ĵ�Բ�뾶Ϊ![]() ��СԲ�뾶Ϊ2�����������͡���y������ʱ��
��СԲ�뾶Ϊ2�����������͡���y������ʱ��![]() �����������͡���ֱ��
�����������͡���ֱ��![]() ����ʱ����֪�е�Ϊ��10��4������ʱB��10��0����
����ʱ����֪�е�Ϊ��10��4������ʱB��10��0����![]() �������Ƴ���
�������Ƴ���![]() ʱ���߶�AB�����С����µ㡱����
ʱ���߶�AB�����С����µ㡱����![]() �ڲ���
�ڲ���
���������ͼ3�У�ֱ��PG���߶�AB���ȷ֣�����ֱ��PG����Q��2��0��ʱ��ֱ��PG�Ľ���ʽΪ![]() ����
����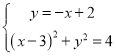 ���
���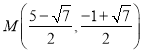 ����
����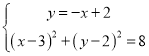 �����
�����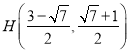 �����ɵõ�P�ĺ�����ķ�Χ.
�����ɵõ�P�ĺ�����ķ�Χ.
����ֱ��PG����F��4��0��ʱ��ͬ������.
��1������ͼ1��
����֪��֪AE=BE=4����EAB=90�㣬
���AEB=��ABE=45�㣬
AF=DF=3����AFD=90�㣬���DAF=45�㣬
���DAF+��ABE=90�㣬
���AHB=90�㣬
���ADB<90�㣬��ACB>90�㣬
���߶�AB�ġ����µ㡱��D��E��
�ʴ�ΪD��E��
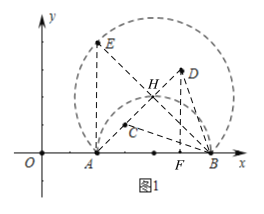
����ͼ2�У�
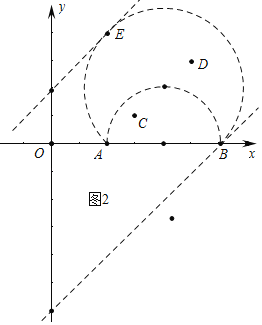
����ֱ��![]() ������B��6��0��ʱ��
������B��6��0��ʱ��![]() ��
��
����ֱ����![]() ����ʱ����
����ʱ����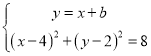 ��
��
��ȥy�����õ�![]() ��
��
������![]() ���ɵ�
���ɵ�![]() �����
�����![]() ��6��
��6��
������������ֱ��![]() �ϴ����߶�AB�ġ����µ㡱��b��ȡֵ��ΧΪ
�ϴ����߶�AB�ġ����µ㡱��b��ȡֵ��ΧΪ![]() ��
��
��3������һ����ͼ�����Ͽ�֪��ԲAB���е�QΪ�������͡��Ĵ�Բ��Բ�ģ�
�����͡���Բ�İ뾶Ϊ![]() ��СԲ�뾶Ϊ2��
��СԲ�뾶Ϊ2��
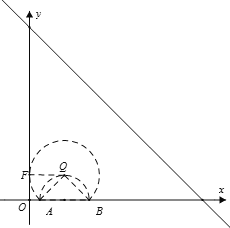
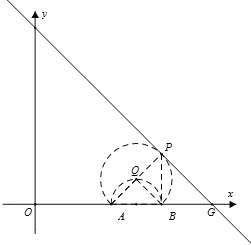
���������͡���y������ʱ����QF��y��ʱ����ʱQF=2![]() ����
����![]() ��
��
���������͡���ֱ��![]() ����ʱ����AP��ֱ��y=-x+14��
����ʱ����AP��ֱ��y=-x+14��
��ʱ�е�ΪP����PBA=90�㣬
��ֱ��y=-x+14��x��ļнǡ�PGB=45�㣬
���PAB=45�㣬
���PAGΪ����ֱ�������Σ�
��BG=PB=AB=4��
��y=0ʱ��0=-x+14�����x=14����G��14��0����
��P��10��4����B��10��0����A��6��0��
��![]() ��
��
�൱![]() ʱ���߶�AB�����С����µ㡱���ڡ�MON�ڲ���
ʱ���߶�AB�����С����µ㡱���ڡ�MON�ڲ���
����2����ͼ3�У�
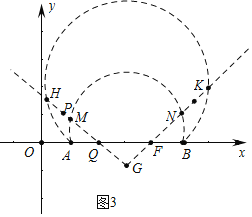
��ֱ��PG���߶�AB���ȷ֣�
����ֱ��PG����Q��2��0��ʱ��
ֱ��PG�Ľ���ʽΪ![]() ��
��
��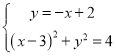 �����
�����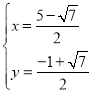 ��
�� ����ȥ����
����ȥ����
��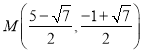 ��
��
��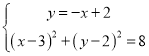 �����
�����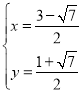 ��
��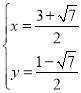 ����ȥ����
����ȥ����
��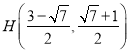 ��
��
���P�ĺ�����ķ�ΧΪ![]() ��
��
����ֱ��PG����F��4��0��ʱ��
ֱ��PG�Ľ���ʽΪ![]() ��ͬ���ɵõ�P�ĺ������ȡֵ��ΧΪ
��ͬ���ɵõ�P�ĺ������ȡֵ��ΧΪ![]() ��
��
�������������������ĵ�P�ĺ������ȡֵ��ΧΪ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
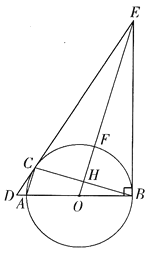
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬����C����O�����ߣ���BA���ӳ��߽��ڵ�D������B��BE��BA����DC�ӳ����ڵ�E������OE������O�ڵ�F����BC�ڵ�H������AC��
��1����֤����ECB����EBC��
��2������BF��CF����CF��6��sin��FCB=![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
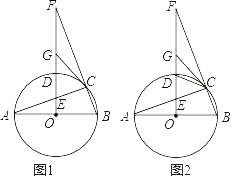
����Ŀ����ͼ1����֪AB����O��ֱ����AC����O���ң���O����OF��AB����O�ڵ�D����AC�ڵ�E����BC���ӳ����ڵ�F����G��EF���е㣬����CG
(1)�ж�CG����O��λ�ù�ϵ����˵�����ɣ�
(2)��֤��2OB2��BCBF��
(3)��ͼ2������DCE��2��F��CE��3��DG��2.5ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��Ŵ��ж�ʮ�Ľ����裬�����꾪������죬����â�����������ﴦ¶�ﺮ˪������ѩѩ��С��������Ϊ���ڼ����ҹ���ʱ�����ж�ʮ�Ľ�������ɵ�Сʫ�裬����������ָ��ʮ��ʱ�ں��������й��Ŵ�������һ������ָ��ũ�µIJ������������й��Ŵ��Ͷ������ھ���Ļ��ۺ��ǻ۵Ľᾧ�����е�һ������������ָ������Ϊ�����Ŀ�ʼ����������ѧ�ϵ��봺�������ϸ���ģ�������5�����ƽ�������ȶ�����![]() �ֵ���
�ֵ���![]() �������ǽ��봺�죬���У�5���еĵ�һ�켴Ϊ�봺�գ����磺2014��3��13����18�գ���������ƽ�����·ֱ�Ϊ
�������ǽ��봺�죬���У�5���еĵ�һ�켴Ϊ�봺�գ����磺2014��3��13����18�գ���������ƽ�����·ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������3��14�տ�ʼ��������ƽ������������5���ȶ�����
������3��14�տ�ʼ��������ƽ������������5���ȶ�����![]() ���ﵽ������ѧ�����ϵ��봺������˿���˵2014��3��14��Ϊ�������봺�գ���ƽ���¶���ָһ��24Сʱ��ƽ���¶ȣ�����ѧ��ͨ����һ���е�2ʱ��8ʱ��14ʱ��20ʱ4��ʱ�̵����µ�ƽ��ֵ��Ϊ��һ�����ƽ������(��4��������ӳ���4)���������һλС��������DZ���˳��2017��3��28����4��3�յ����¼�¼����ƽ������(��λ��
���ﵽ������ѧ�����ϵ��봺������˿���˵2014��3��14��Ϊ�������봺�գ���ƽ���¶���ָһ��24Сʱ��ƽ���¶ȣ�����ѧ��ͨ����һ���е�2ʱ��8ʱ��14ʱ��20ʱ4��ʱ�̵����µ�ƽ��ֵ��Ϊ��һ�����ƽ������(��4��������ӳ���4)���������һλС��������DZ���˳��2017��3��28����4��3�յ����¼�¼����ƽ������(��λ��![]() )
)
ʱ�� | 2ʱ | 8ʱ | 14ʱ | 20ʱ | ƽ������ |
3��28�� | 6 | 8 | 13 | 11 | 9.5 |
3��29�� | 7 | 6 | 17 | 14 | a |
3��30�� | 7 | 9 | 15 | 12 | 10.8 |
3��31�� | 8 | 10 | 19 | 13 | 12.5 |
4��1�� | 8 | 7 | 18 | 15 | 12 |
4��2�� | 11 | 7 | 22 | 16 | 14 |
4��3�� | 13 | 11 | 21 | 17 | 15.5 |
�������ϲ��Ͻ���������⣺
(1)���3��29�յ���ƽ������![]() ��
��
(2)�����ʵ���ͳ��ͼ����7�����ƽ�����µı仯�����ʾ������
(3)��ָ��2017�����һ���DZ���˳��������ѧ�����ϵ��봺�գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
������ȫ��Ψһһ��ȫ������ˮԴ�����ص�����ɭ�ָ����ʴﵽ57.46%�����ɾ�ָ������������ȫ�е�һ���˾������̵����41.88ƽ���ף������������ڱ���ȫ��ǰ�У������������ֵĿ���������ͨ����2012���������Ϊ�ţ���Ϊ���������˾ӵĵط���
���ھ��÷�չ��˽�ҳ�������ԭ��2013����������½�Ϊ����������PM2.5ƽ��Ũ������������2013��PM2.5ƽ��Ũ��ԼΪ78��/�����ף���2012��PM2.5ƽ��Ũ��������12.2%����������Ϊ2019�������2022�궬�»�����ľٰ�أ���ȫ��������ú����������������PM2.5Ũ�ȣ�������2020�꽵��46��/�����ף�ʵ�֡�����������
��Ϥ�����콫�����ƹ��Դ�ȱá����ܡ�̫���ܵ�����Դ�Ϳ�������Դ��ͬʱǿ���������ܣ���������Դ���������ʣ�2020������Դ�Ϳ�������Դ�������ʹ�ñ������ﵽ40%��ú̿��Դ��������ռ��3%���£��������ɡ���ú������
����ȫ��������2014��PM2.5ƽ��Ũ��ԼΪ70��/�����ף���2013��ƽ��Ũ�Ƚ�����10.26%��2015��PM2.5ƽ��Ũ�ȱ�2014��ƽ��Ũ�Ƚ�����10%��Ϊȫ����ͣ�2016��PM2.5ƽ��Ũ��ԼΪ56��/�����ף�
�������ϲ��Ͻ���������⣺
��1��2015��PM2.5ƽ��Ũ��ԼΪ ��/�����ף�
��2��ѡ��ͳ�Ʊ���ͳ��ͼ����2013��2016��PM2.5ƽ��Ũ������������
��3�������������Ϻͻ��Ƶ�ͳ�Ʊ���ͳ��ͼ���ṩ����Ϣ��Ԥ��2017���PM2.5ƽ��Ũ��ԼΪ ��/�����ף����Ԥ�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����գ��������������������ˡ������пɳ�����չ�滮���������Ҫ���ɳ�����չ��ȫ���³��е�Ŀ�꣬ij����ѧУ�˽�ѧ���Ĵ�����ʶ����֯��ȫУѧ���μӴ����������������г�ȡ�˲���ѧ���ɼ�����Ϊ5�飺A��50��60��B��60��70��C��70��80��D��80��90��E��90��100��ͳ�ƺ�õ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ��ÿ�麬��Сֵ�������ֵ��������ͳ��ͼ��
��1����ȡѧ�������������� ���ˣ�����C��Բ�Ľ����� ���㣻
��2����ȫƵ��ֱ��ͼ��
��3����У����2200��ѧ�������ɼ���70�����£�����70�֣���ѧ��������ʶ��ǿ���д���һ�����������У������ʶ��ǿ��ѧ��Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
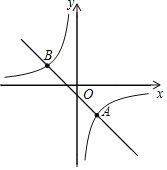
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��y=kx+b��k��0����˫����y=![]() ��m��0�����ڵ�A��2��-3���͵�B��n��2����
��m��0�����ڵ�A��2��-3���͵�B��n��2����
��1����ֱ����˫���ߵı���ʽ��
��2����P��˫����y=![]() ��m��0���ϵĵ㣬��ᡢ�����궼������������P��x��Ĵ��ߣ���ֱ��AB�ڵ�Q������Pλ�ڵ�Q�·�ʱ����ֱ��д����P�����꣮
��m��0���ϵĵ㣬��ᡢ�����궼������������P��x��Ĵ��ߣ���ֱ��AB�ڵ�Q������Pλ�ڵ�Q�·�ʱ����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ij�����꼶��ʦ���Ծ������ε�ѧ������Ƚ������۵��飬��������ĿΪ�������ɡ�����˼����רע������������Ŀ��������������ȡ��������ͬѧ�IJ�����������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ�������������������ͼ��������Ϣ����������⣺
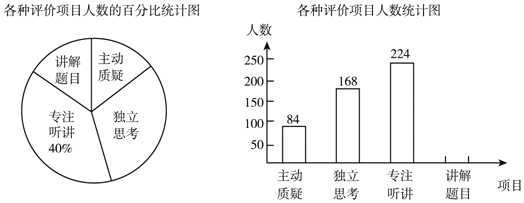
(1)����������У�һ��������� ����ͬѧ��
(2)�뽫����ͳ��ͼ����������
(3)���ȫ����6000�����꼶ѧ������ô���Ծ��������У�������˼������Լ�ж����ˣ�
(4)����ͳ�Ʒ�ӳ�����������Ը����ľ��꼶ͬѧ���һ���Դ��Ծ������εĽ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
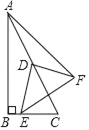
����Ŀ����ͼ����Rt��ABC�У���ABC��90�㣬��BAC��30�㣬BC��2����D��AC�ߵ��е㣬E��ֱ��BC��һ���㣬���߶�DE�Ƶ�D��ʱ����ת90��õ��߶�DF������AF��EF���ڵ�E���˶��������߶�AF����СֵΪ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com