
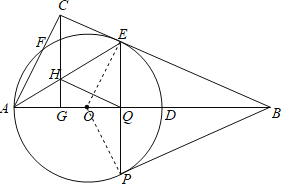
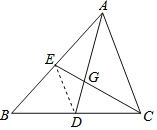
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,交AC于点F,过点C作CG⊥AB交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为⊙O的切线.
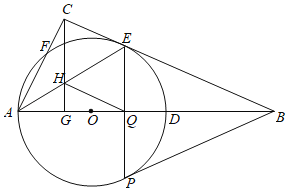
(1)求证:BC是⊙O的切线.
(2)求证:![]() =
=![]() .
.
(3)若sin∠ABC═![]() ,AC=15,求四边形CHQE的面积.
,AC=15,求四边形CHQE的面积.
【答案】(1)见解析;(2)见解析;(3)45
【解析】
(1)连接OE,OP,根据线段垂直平分线的性质得到PB=BE,根据全等三角形的性质得到∠BEO=∠BPO,根据切线的判定和性质定理即可得到结论.
(2)根据平行线和等腰三角形的性质即可得到结论.
(3)根据垂径定理得到EP⊥AB,根据平行线和等腰三角形的性质得到∠CAE=∠EAO,根据全等三角形的性质得到CE=QE,推出四边形CHQE是菱形,解直角三角形得到CG=![]() =12,根据勾股定理即可得到结论.
=12,根据勾股定理即可得到结论.
(1)证明:连接OE,OP,
∵PE⊥AB,点Q为弦EP的中点,
∴AB垂直平分EP,
∴PB=BE,
∵OE=OP,OB=OB,
∴△BEO≌△BPO(SSS),
∴∠BEO=∠BPO,
∵BP为⊙O的切线,
∴∠BPO=90°,
∴∠BEO=90°,
∴OE⊥BC,
∴BC是⊙O的切线.
(2)解:∵∠BEO=∠ACB=90°,
∴AC∥OE,
∴∠CAE=∠OEA,
∵OA=OE,
∴∠EAO=∠AEO,
∴∠CAE=∠EAO,
∴![]() .
.
(3)解:∵AD为的⊙O直径,点Q为弦EP的中点,
∴EP⊥AB,
∵CG⊥AB,
∴CG∥EP,
∵∠ACB=∠BEO=90°,
∴AC∥OE,
∴∠CAE=∠AEO,
∵OA=OE,
∴∠EAQ=∠AEO,
∴∠CAE=∠EAO,
∵∠ACE=∠AQE=90°,AE=AE,
∴△ACE≌△AQE(AAS),
∴CE=QE,
∵∠AEC+∠CAE=∠EAQ+∠AHG=90°,
∴∠CEH=∠AHG,
∵∠AHG=∠CHE,
∴∠CHE=∠CEH,
∴CH=CE,
∴CH=EQ,
∴四边形CHQE是平行四边形,
∵CH=CE,
∴四边形CHQE是菱形,
∵sin∠ABC═sin∠ACG═![]() =
=![]() ,
,
∵AC=15,
∴AG=9,
∴CG=![]() =12,
=12,
∵△ACE≌△AQE,
∴AQ=AC=15,
∴QG=6,
∵HQ2=HG2+QG2,
∴HQ2=(12﹣HQ)2+62,
解得:HQ=![]() ,
,
∴CH=HQ=![]() ,
,
∴四边形CHQE的面积=CHGQ=![]() ×6=45.
×6=45.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
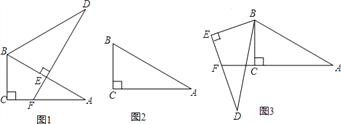
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.![]() 为抛物线上一动点(不与点
为抛物线上一动点(不与点![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方时,过点
上方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,请直接写出点
为顶点的四边形能否构成平行四边形?若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
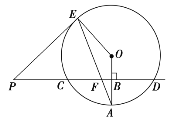
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)若PF=13,求PE的长;
(3)在(2)的条件下,sinA=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
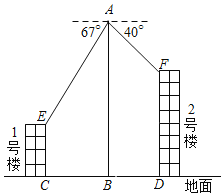
【题目】在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
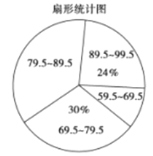
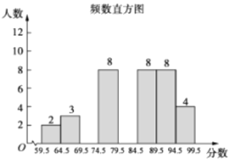
(1)本次比赛参赛选手共有________人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为________;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有4张正面分别写有数字1、2、3、4的卡片,将4张卡片的背面朝上,洗匀.
(1)若从中任意抽取1张,抽的卡片上的数字恰好为3的概率是________;
(2)若先从中任意抽取1张(不放回),再从余下的3张中任意抽取1张,求抽得的2张卡片上的数字之和为3的倍数的概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2021年起,江苏省高考采用“![]() ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是________;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
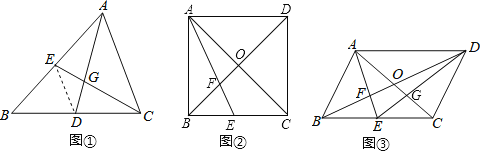
【题目】教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 相交于点
相交于点![]() ,求证:
,求证:![]() ,
,
证明:连结![]() .
.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图②,若![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 的长为 .
的长为 .
(2)如图③,连结![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 .
的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com