
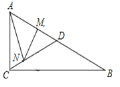
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 向终点
向终点![]() 运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为
运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() (平方单位),则
(平方单位),则![]() 与
与![]() 之间的图象大致为( )
之间的图象大致为( )
A.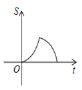 B.
B. C.
C.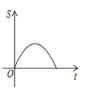 D.
D.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
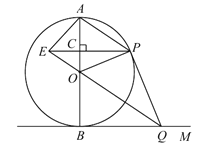
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() 两点重合),连接
两点重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() .
.
(2)若直径![]() 的长为12.
的长为12.
①当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;
②当![]() ________时,四边形
________时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )

A.4B.5C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植树4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数和中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
科目:初中数学 来源: 题型:
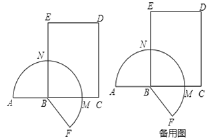
【题目】如图,点![]() 为长为5的线段
为长为5的线段![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,且
,且![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,将线段
,将线段![]() 绕点B顺时针旋转,得到线段
绕点B顺时针旋转,得到线段![]() ,优弧
,优弧![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,设旋转角为
,设旋转角为![]()
(1)若扇形![]() 的面积为
的面积为![]() ,则
,则![]() 的度数为_______.
的度数为_______.
(2)连接![]() ,判断
,判断![]() 与扇形
与扇形![]() 所在圆
所在圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设![]() 为直线
为直线![]() 上一点,沿
上一点,沿![]() 所在直线折叠矩形,若折叠
所在直线折叠矩形,若折叠![]() 后所在的直线与扇形
后所在的直线与扇形![]() 所在
所在![]() 的相切,求
的相切,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c时,⊙O恰好自转1周.

(2)如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的角∠O1BO2 = n°,⊙O在点B处自转![]() 周.
周.

实践应用:
(1)在阅读理解的(1)中,若AB=2c,则⊙O自转 周;若AB=l,则⊙O自转 周.在阅读理解的(2)中,若∠ABC= 120°,则⊙O在点B处自转 周;若∠ABC= 60°,则⊙O在点B处自转 周.
(2)如图13-3,∠ABC=90°,AB=BC=![]() c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.

拓展联想:
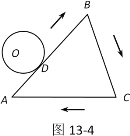
(1)如图13-4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
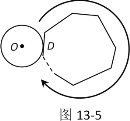
(2)如图13-5,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场今年2月份营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )
A.633.6(1+x)2=400(1+10%)B.633.6(1+2x)2=400×(1010%)
C.400×(1+10%)(1+2x)2=633.6D.400×(1+10%)(1+x)2=633.6
查看答案和解析>>
科目:初中数学 来源: 题型:
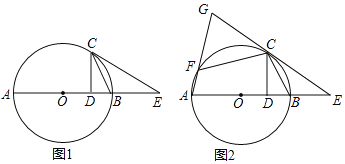
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,连接CB,过C作CD⊥AB于点D,过点C作∠BCE,使∠BCE=∠BCD,其中CE交AB的延长线于点E.
(1)求证:CE是⊙O的切线.
(2)如图2,点F在⊙O上,且满足∠FCE=2∠ABC,连接AF井延长交EC的延长线于点G.
①试探究线段CF与CD之间满足的数量关系;
②若CD=4,BD=2,求线段FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com